
- •26.Теорема о связи функции, её предела и бесконечно малой функции.
- •27.Бесконечно большие и бесконечно малые функции, их свойства.
- •28.Сравнение бесконечно малых функций, эквивалентные бесконечно малые функции, их свойства.
- •29.Первый и второй замечательный предел функции.
- •30.Непрерывность функций. Точки разрыва функции, их классификация.
- •31.Свойства функций непрерывных на отрезке.
- •32. Производная. Её геометрический и механический смысл.
- •33.Основные правила дифференцирования. Производная сложной функции, производная обратной функции. Производная неявно заданной функции. Производная функции, заданной параметрически.
- •34.Связь между непрерывностью и дифференцируемостью функции.
- •35.Теоремы о дифференцируемых функциях (Ролля, Лагранжа, Коши, Лопиталя)
- •36.Дифференциал функции и его приложения.
- •37. Условия возрастания и убывания функций. Экстремумы.
- •38. Выпуклость. Точки перегиба. Достаточное условие существования точек перегиба
- •39.Асимптоты графика функции.
- •40. Наибольшее и наименьшее значение непрерывной на отрезке функции.
- •41. Понятие функции нескольких переменных. Предел функции двух переменных.
- •42.Частные производные функции двух переменных.
- •43.Частные производные высших порядков функции двух переменных.
- •44.Экстремумы функций двух переменных. Необходимые и достаточные условия экстремума.
- •45.Наибольшее и наименьшее значение функции двух переменных в замкнутой ограниченной области.
26.Теорема о связи функции, её предела и бесконечно малой функции.
Если
функция ƒ(х) имеем предел, равный b,
то ее можно представить как сумму числа
b
и бесконечно малой функции α(х), т.е.![]() ,
то
ƒ(х)=b+α(х),
где α(х)- бесконечно малая величина.
,
то
ƒ(х)=b+α(х),
где α(х)- бесконечно малая величина.
Док-во:
Пусть
![]() тогда
тогда
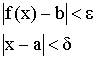
![]() ,
значит
,
значит
![]() ,
,
![]() –
бесконечно малая величина.
–
бесконечно малая величина.
27.Бесконечно большие и бесконечно малые функции, их свойства.
Бесконечно малая функция:
Последовательность
![]() называется бесконечно
малой,
если
называется бесконечно
малой,
если
![]() .
.
Например,
последовательность чисел
![]() — бесконечно малая. Функция называется
бесконечно
малой в окрестности
точки x0,
если
— бесконечно малая. Функция называется
бесконечно
малой в окрестности
точки x0,
если
![]() .
Функция называется бесконечно
малой на бесконечности,
если
.
Функция называется бесконечно
малой на бесконечности,
если
![]() либо
либо
![]() .
Также бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если
.
Также бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если
![]() , то
, то
![]() ,
,
![]() .
Бесконечно
большая функция:
.
Бесконечно
большая функция:
Последовательность
называется бесконечно
большой, если
![]() .
.
Функция называется бесконечно большой в окрестности точки х0, если
![]() .
Функция называется бесконечно
большой на
бесконечности,
если
.
Функция называется бесконечно
большой на
бесконечности,
если
![]() либо
либо
![]() .
.
Свойства:
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если — бесконечно малая последовательность, сохраняющая знак, то
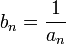 — бесконечно большая последовательность.
— бесконечно большая последовательность.
28.Сравнение бесконечно малых функций, эквивалентные бесконечно малые функции, их свойства.
Общим у всех бесконечно малых функций явл. их стремление к нулю, однако «скорость» стремления к нулю может быть различной.
Пусть
α(х) и β(х)- бесконечно малые, при х→х0
функции, если 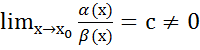 ,
то говорят, что α(х) и β(х)- одного порядка
малости. Если же
,
то говорят, что α(х) и β(х)- одного порядка
малости. Если же 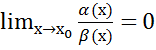 ,
то говорят, что α(х)-бесконечно малая
более высокого порядка малости, чем
β(х) и пишут α(х)=0(β(х)).
,
то говорят, что α(х)-бесконечно малая
более высокого порядка малости, чем
β(х) и пишут α(х)=0(β(х)).
Бесконечно
малые функцииα(x)
иβ(x)
называются эквивалентными при x![]() a,
если
a,
если
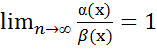 .
Если α(х) – бесконечно малая функция,
то справедливы основные эквивалентности:
sinα(x)~α(x);
tgα(x)~α(x);arcsinα(x)~
α(x);
arctgα(x)~α(x);
eα(x)
.
Если α(х) – бесконечно малая функция,
то справедливы основные эквивалентности:
sinα(x)~α(x);
tgα(x)~α(x);arcsinα(x)~
α(x);
arctgα(x)~α(x);
eα(x)![]() ~α(x);
ln(1+α(x))~α(x);
aα(x)
~α(x)*lnα;
~α(x);
ln(1+α(x))~α(x);
aα(x)
~α(x)*lnα;
![]() .
При вычислении пределов используются
следующие теоремы об эквивалентных
бесконечно малых функциях:
.
При вычислении пределов используются
следующие теоремы об эквивалентных
бесконечно малых функциях:
Т1) Предел отношения двух бесконечно малых функций равен пределу отношения функций, им эквивалентных,
Т2) Сумма нескольких бесконечно малых функций различных порядков малости эквивалентна слагаемому низшего порядка малости.
29.Первый и второй замечательный предел функции.
Первый и второй замечательный предел используют для раскрытия неопределенностей, содержащих тригонометрические функции
Первый
замечательный предел.
![]()
Второй
замечательный предел.
![]()
Док-во первого:
Рассм.
Окружность единичного радиуса и < х €
(0;![]() )
)
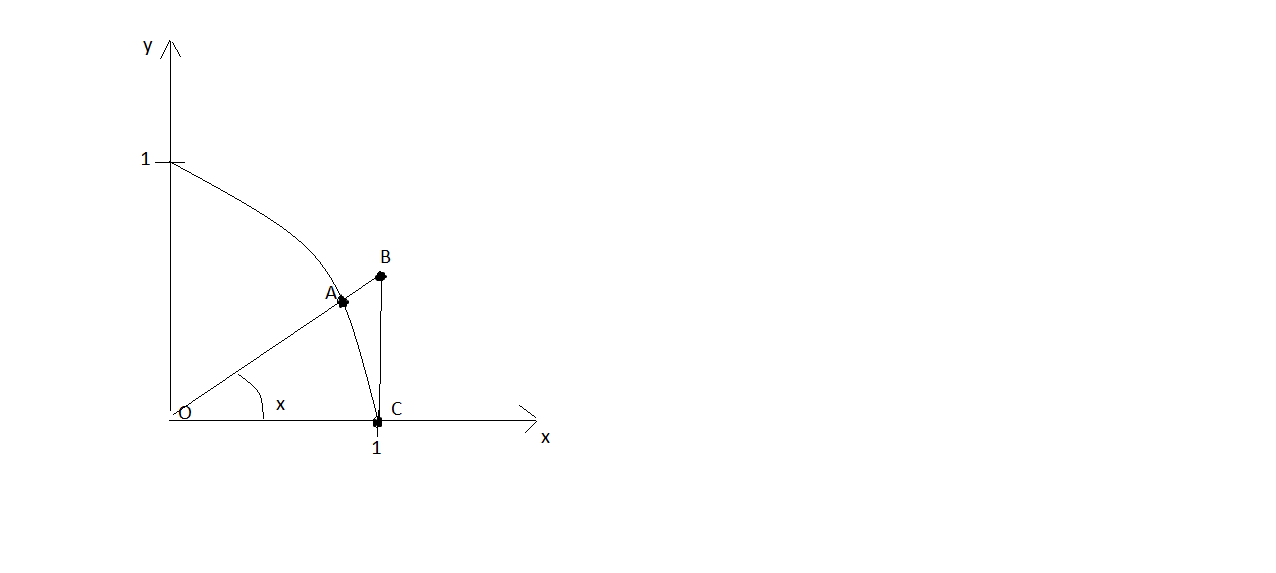 Из
рис. следует, что:
Из
рис. следует, что:
![]()
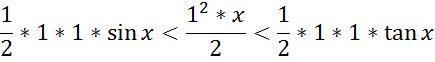
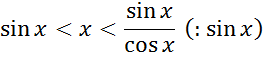
1<![]()
Значит (перейдём к обратным):
1<![]() >
>
![]()
Если
х
€
(-![]() ,
то –х
€
(0;
,
то –х
€
(0;![]() ,
тогда:
,
тогда:
1
> ![]()
Таким
образом неравенство справедливы для
любого х
€
(-![]() отличного от нуля. Т.к.
отличного от нуля. Т.к. ![]() ,
,
![]() ,
то
,
то ![]()
Док-во второго:
Сделав
во втором замечательном пределе замену
![]() = t,
получим
= t,
получим ![]() = е.
= е.
