Формирование тарифов

В ОСАГО используется большой список коэффициентов, применяемых в базовой тарифной ставке: коэффициент территории, бонус-малус, возраста и стажа, количества лиц, допущенных к управлению, мощности двигателя транспортного средства, периода использования.

Бонус-Малус (КБМ)

M 0 1 2 3 4 … 13

2,4 2,3 1,5 1,4 1 0,95 … 0,05

0 1 2 3

Наряду с ОСАГО страховые компании предлагают ДОСАГО с относительно не высоким страховым взносом и более привлекательными страхователю суммами.

При выезде за рубеж на транспортном средстве необходимо приобретать полис в рамках системы зелёная карта. В зависимости от государства страховая сумма может быть как неограниченной, так и ограниченной. Такие полисы продаются также в РФ, однако не все компании включены в эту систему.

Расчёт тарифов предпринимательских рисков

Виды предпринимательских рисков:

• страхование убытков по единица продаж

• депозитов

• банков невозврата кредитов

• остановок производства

• инноваций – венчурного бизнеса

• рисков снижения объемов продаж или увеличение расходов

• страхование урожаев

Все эти виды страхования страхуют потери, которые произошли не по вине страхователя. Страховщик имеет право контролировать прочес соблюдения технологий норм.

На примере страхования урожаев

X-сам урожай

FК-функция распределения величины урожая.

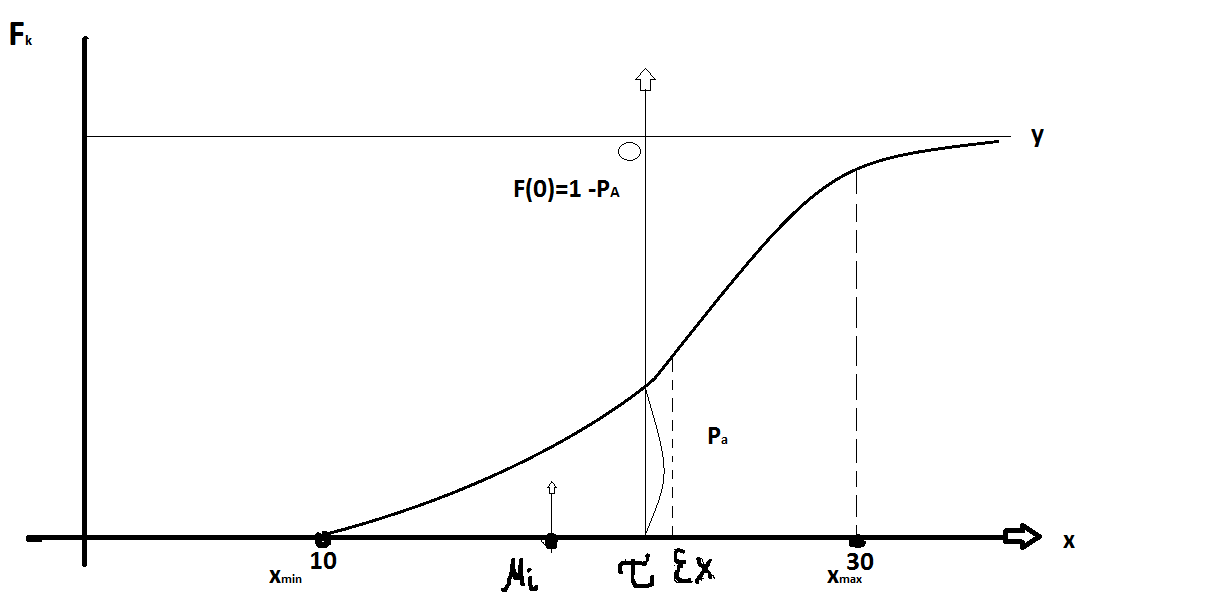
В качестве ориентира вводится ф-я потерь. За ориентир принимается некоторая средняя , f-франшиза, ,

величина обратная по отношения к ф-ции х

Fy=1-Fx

dFy = - fFx

ML – средние потери

EL –ожидаемые потери, они меньше чем средние

EL=ML-pa

Событие

Х Y

0

0

Ф-я потерь 1 и 2 способ соответсвенно

1)

Таким образом

EL=F нижний частный момент порядка 1, относительно

2) ;

dFy = -dFx

EL=E(Y|I)pa ; E(Y|I) ML

Модель коллективного риска и стохастическое ур-ние динамики страховых резервов.

Составной Пуассоновский процесс N(t)

Zi = Ki Ii Si

n – договоров

EIi = p

Модель коллективного риска имеют следующие допущения:

1. процесс поступления рисков растянут во времени. У нее есть динамика, при это не рассматривается вероятность индивидуальных рисков (нет n и p).

2. Размеры выплат друг от друга не зависят

3. В страх. компанию поступает непрерывно во времени приток договоров с некоторой интенсивностью.

В этих моделях рассмотрим динамику резервов.

Задача: ставится задача исследовать вероятность разорения компании (резервы станут <0) в зависимости от стартового капитала и страховой премии, величины страхового тарифа.

Yt –диск переменная – стартовый капитал страховщика

у + ct -

с – страховая премия

t – время

N(t) – случайная величина, кол-во рисков

Z=

N=

Z= ; N=1,2,3……

Будем считать, что все Zn друг от друга не зависят и все они одинаковы.

Sn=1 , Rn-одинаковые

Zn=Rn

Z=

ER =

ED=

EN

DN=

Надо найти EZ, DZ

Если бы Z=NR, то как неоднородный портфель (???)

EZ= * (???)

EZ= ) * p(N=n)

= =

=ER = ER EN

EN

DZ =

интенсивность, скорость

E(ct)=EZ= , тогда C= , С - страховая премия, тариф.

C= *(1+ )

Т Т0 Т+r

вероятность, величина разорения

=p(Yt

Если Y0<0 , то =1

N(t) – представляет собой пуассоновский процесс

P(N(t) = e

N(t)

T

-среднее время между 2 скачками

T-время между событиями

Ezt= (???)

Величину можно получить решая интегрально дифференциальное уравнение и если Z распределеятеся по экспоненциальному закону F(Zt Z) = 1- e , то имеется решение:

Если y =0 , то

-средние суммы, на которые мы страхуем

В общем случае имеет место неравенство Крамера-Лундберга

Где R -положительный корень интегрального уравнения

x=0,1….

генерирует поток событий

t

- время между событиями

Так же потоки являются аппаратами массового обслуживания.

Простейший пуассоновский поток – процесс с независимыми приращениями

Этот поток обладает св-ми

1)стационарность, т.е. вероятность появления х событий на интервале (t; t+ )

Зависит от -ширины интервала и от х, но от t не зависит. Пара (х; ) определяет интенсивность событий.

постоянна, потому поток стационарен

2) отсутствие последействия – предыстория не влияет на вероятности появления событий в будущем. Только начальное состояние влияет на будущее, прошлое не имеет значения, его нет.

3)ординарность, т.е. вероятность появления в некотором «малом» интервале времени более чем одного события почти равна 0. Эта вероятность на порядок меньше, чем вероятность вообще ни одного события или одного события.

- среднее время между события малость означает , что T <<1

Следствием из этих св-в является то, что интервалы времени между событиями распределены экспоненциально. расположены экспоненциально

Проверка св-в

1)

Разложим е в ряд Тейлора и будем считать, что , т.е -величина маленькая.

А если , то является величиной второго порядка малости.

означает, что интервал

T=среднее время между отдельными событиями

Из проверки видно, что интервалы времени распределены по экспоненциальному закону.

Т.к от t не зависит, то можно положить, что t=0

Это означает, что ф-я распределения

Кривая