Методы определения тарифов в рисковых видах страхования. !3!

Модель индивидуального риска.

Этот подход основывается на следующих предпосылках:

1. здесь не учитывается фактор времени

2. у населения есть некоторое фиксированное кол-во договоров

3. рассчитывается нетто-тариф – чистая тарифная ставка

4. на данном временном интервале страховая компания работает безубыточно с достаточно большой вероятностью

Z – суммарный риск

Q – суммарная премия

β ≈ 1 – вероятность того, что суммарный риск будет меньше, чем суммарная премия с большой вероятностью

α = (1 - β) << 1 – риск разорения

P (Z>Q) = α

Проведём стандартизацию для P(Z≤Q) = β

P = β

F

(*)

Если Z = ∑zi (но Z≠nz) в соответствии с ЦПТ при достаточно больших n функция F стремится к Ф

F→Ф

→N(0;1)

→ - β-квантиль

Величина Q состоит из 2-х частей: в ней есть EZ – ожидаемые убытки и вторая часть, которая связана с

Мы должны помимо средней величины взять надбавку

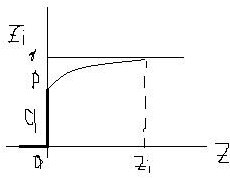
Zi – вкл. сам факт события, ущерб

Zi можно представить в виде произведения: Zi = Ii ∙ Ri ∙ Si

Si – величина неслучайная (предел ответственности страховщика)

Ri – сл. вел. тяжести ущерба, т.е. Ri

Ii – бернулевская сл. вел.- ндикатор события

Однородый (простейший) страховой портфель

1. все Ri = 1

2. Si = S

3. pi = p, qi = q, т.е. pi и qi равны

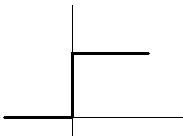
Распределение биномиальное

Положим Ri = 1 и Si= 1

Z = ∑zi = S ∑Ii – сл.вел. подчинена биномиальному закону распределения и представляет собой сумму индикаторов

События независимы

EZ = Snp

DZ = S²npq

Подставим эти выражения в формулу (*):

nST = Q = Snp +

Q – общестраховая премия

Т – страховой тариф – сколько плачу с рубля за 1руб страховой суммы

Найдём Т:

T = p

- основная часть тарифной ставки (=p)

- рисковая надбавка (= )

- относительная рисковая надбавка = , необходима для того, чтобы установить запас устойчивости страховой компании к колебаниям убыточности

Пусть дано 100 договоров, р = 6%. →В среднем будет предъявлено 6 рисков, но на самом деле может быть предъявлено 3, 4, 5, 6, 7,…

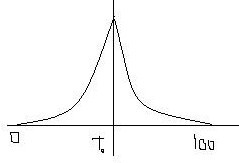np = 6

- коэф.вариации, q≈1

Чем меньше р, тем больше должно быть n; чем больше q, тем меньше p, тем больше ассиметрия, тем больше коэф.вариации

T =

=

особо не влияет на тариф

q≈1 – тоже не влияет на тариф

влияет только np

Чтобы увеличить Т нужно увеличить n. Процесс увеличения n называется диверсификацией.

Неоднородный страховой портфель

Все Si – разные и если страховой случай произошёл, то на всю страховую сумму.

Введём и

EZ = np DZ = ²npq

Q = nT

nT =

T =

= - коэф.,учитывающий неоднородность страхового портфеля

1< <√n

Реалистичный (реальный) страховой портфель

Zi=IiRiSi

Ri- тяжесть ущерба. Ii либо p либо q.

Si – разные, 0<Ri≤1

Для всех i R одна и та же: Ri =R

I, R не зависят друг от друга

ER = μ DR = σ²

Ri могут быть разными, но μ и σ² все одинаковые

EZ =

DZ =

Для независимых: D(IR) = E(IR)² - E²(IR) = E(IR)² - (E²I∙E²R) = E(I)²∙E(R)² - E²I∙E²R = ((E(I²)-E²I+E²I)(E(R²)-E²R+E²R)) – (E²I∙E²R) = (DI+ E²I)(DR+ E²R) – (E²I∙E²R) = DI∙DR + DI∙E²R + DR∙ E²I + E²I∙E²R - E²I∙E²R = DI∙DR + DI∙E²R + E²I∙DR

Для зависимых: D(IR) = DIDR + E²I∙DR + DI∙E²R = pq σ² + p² σ² + μ²pq

q = 1 – p

D(IR) = p σ² + μ²pq

DZ = ( p σ² + μ²pq)

Q = +

T =

T =

- коэф.вариации, так как μ<1, то тариф снижается

Общие принципы формирования страховых тарифов !4!

Страховые тарифы имеют двойственную природу:

• с одной стороны – это плата страховщику за услуги

• с др. стороны он выражает солидарное распределение рисков между страхователями

- тариф-брутто

нагрузка Н -тариф-нетто

-связан с вероятностью и средним ущербом -надбавка рисков, которая связана с дисперсией

- нагрузка в процентах

Нетто-ставка –это основная часть брутто-ставки, предназначенная для формирования страхового фонда для текущих вкладов и создания страховых резервов.

В некоторых видах страхования доля нагрузки доходит до 70% и выше, т.к. основная часть брутто-ставки расходуется на создание резерва предупредительных мероприятий.

Нагрузка идёт на выплату з.п. штатным сотрудникам и кимисионным агентам, на аренду, материальные затраты и в фонд предупредительных мероприятий. Доля нагрузке в брутто-ставке по рисковым видам добровольного страхования не превышает 45%, а по накопительно – сберегатель видом страхование жизни не более 10%.

Часто тарифы рассчитываются и предлагаются централизованно, по страховым компаниям самостоятельно ввести новый вид страхования рассчитать тариф и представить его на утверждение. Кроме того, утверждается структура страхового тарифа. В своей тарифной политике страховщик должен стремиться придерживаться следующих принципов:

1. соблюдение эквивалентности экономических отношений между страховщиком и страхователем за тарифный период (5-10лет). Это значит, что тарифы должны рассчитываться исходя из равенства нетто-премии и суммы страховых выплат. Для этого используется понятие убыточности страховой суммы и считается фактически нагрузка

– страховая премия

- страховые выплаты

Если начинает сильно превышать параметры, то необходимо повышать страховые премии (П).

Убыточность страховых сумм – средняя величина выплат с единицы страховой премии по поводу страхования и в масштабах территории и за определённый период.

2. Соответствие размера страховых тарифов платежеспособность потенциальных страхователей

3. Обеспечение стабильного действия тарифов по данным видам страхования. Если прибыль оказывается больше запланированного, то лучше не снижать тариф, а повысить объем ответственности и увеличить страховые резервы.

4. Гибкость в установлении конкретных страховых тарифов

это можно сделать двумя способами:

1. страховые таривы устанавливаются дифференциально относительно в зависимости от факторов, влияющих на вероятность наступления страхового случая

2. применяются повышающие/понижающие коэффициенты в зависимости от истории страхователя