Классификация страхования по отраслям и видам.
I
Non-life
Life
II
Личное:
Страхование жизни
От несчастных случаев
-детей
-учащихся
-работников
-гос.служащих (обязательное)
-пассажиры
-спортсмены
2. Медицинское
(болезни, операции, лечение в стационаре, страхование в форме ассистанс - для выезжающих за рубеж)
-добровольное
-обязательное
Страхование жизни : дожитие, смерти, пенсии, бракосочетания.
- Имущественное страхование:
1. транспорт – КАСКО
-наземный
-ж\д
-водные
-воздушный
-автомобильный
- погруз (КАРГО)
-здания
2. страхование предпринимательской деятельности
-страхование ожидаемого дохода в денежной\натур форме
-финансовые риски ( риски связанные с рынком: ЦБ)
3. страхование ответственности
(заранее не известно, кто получит страховку)
А) гражданская ответственность
-ОСАГО –обязательное страхование автогражданской ответственности
- перевозчики
-предприятия (источник загрязнения)
Б) за неисполнение обязанностей
В) проф. обязательства
Модель страхования. Позиция страхователя.
P – Вероятность наступления страхового случая
C – Стоимость имущества застрахованного
S – Величина, на которую застраховано имущество =K
d – премия (взнос) страхователя страховщику
-
q
p
Потери EX
DX
σ
Без страхования
0
C
pc
pqc²
c√pq
страхование
d
d+(1-k)C
D+p(1-k)C
(1-k)² с² pq
C(1-k) √pq
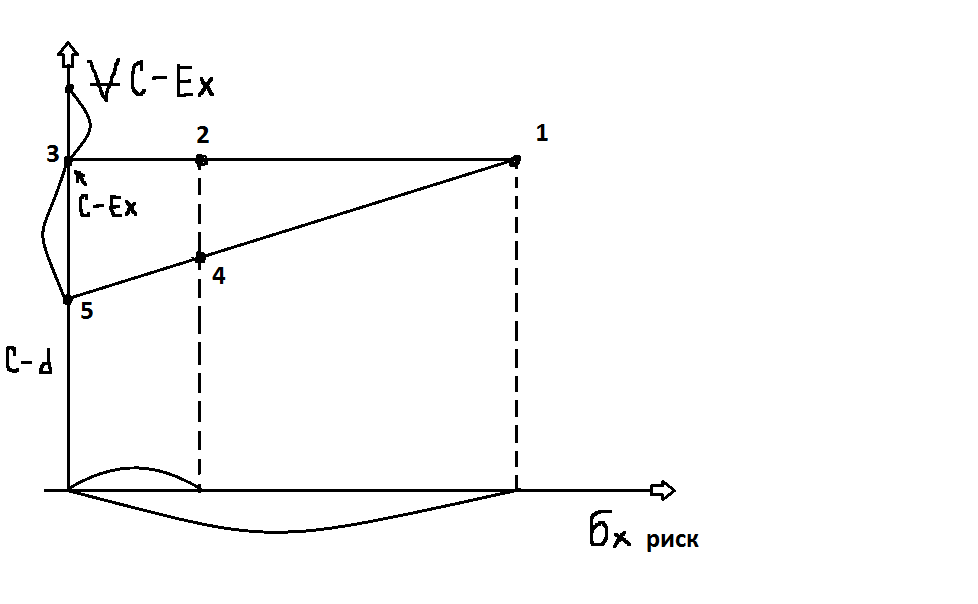d=pc
(.) 2 – страхуем, но K< 1
(.) 3 – идеальный случай, к= 1, риск нулевой
(.) 4 – реальный случай
(.)5 –может быть
Чтобы не уходить с линии: d= pkC
Реально : d>pkc
Когда есть смысл страховать?
Выгодность страховать страхователя связана с тем, насколько доходен его бизнес и какова оценка вероятности ущерба(риска)
Модель системы «страхователь-страховщик».
Y – капитал, который имеет страховщик
C – начальный капитал страхователя
U(), Ui() – функции полезности страховщика \ страхователя
X- возможный ущерб страхователя (случайная величина)
Z – возможный ущерб страховщика (случ величина)
Функция полезности (Госсен)
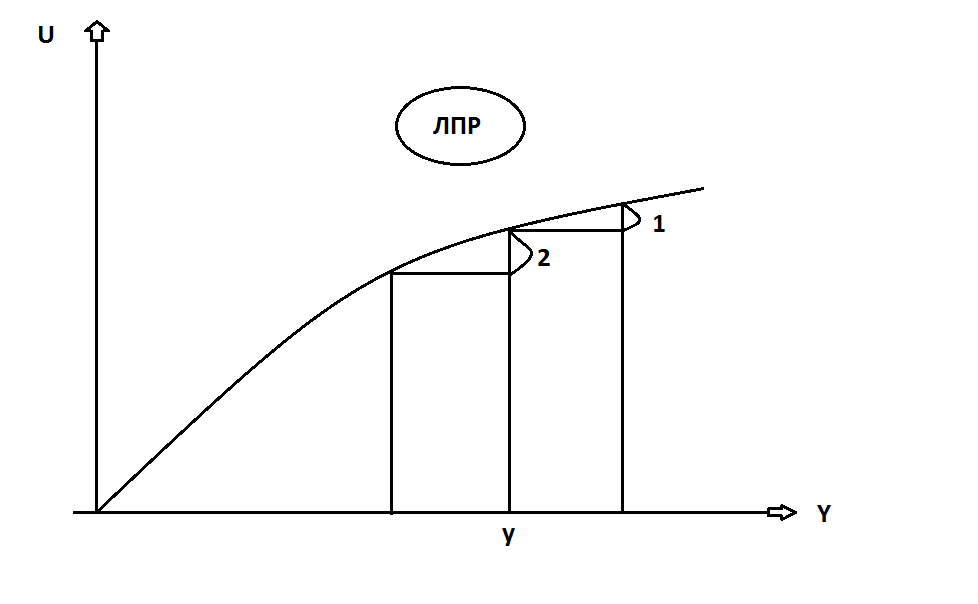
Полезность выигрыша 1 больше, чем полезность выигрыша 2.
Если функция линейная, то ЛПР - ровная линия.
Yi – капитал страхователя
d – взнос, который платит страхователь страховщику
n – количество страхователей
D=n*d = ∑di – суммарные взносы
U( Y+В - ∑ Zi)
Ф1 (d) =EU(Y+D-∑Zi) – U(Y) –приращение полезности для страховщика
C(.) зрения страхователя:
Страхователю выгодно страховать, если его полезность после страхования >, чем полезность без страхования.
E Ui –ожидаемая полезность.
Ф2=Ui(yi-d) –E Ui(yi-Zi)
Ui(yi-d) > E Ui(yi-Zi)
Если Ф2 >0, то стоит страховать.
Для страховщика, чем больше d, тем ему лучше, для страхователя – наоборот.
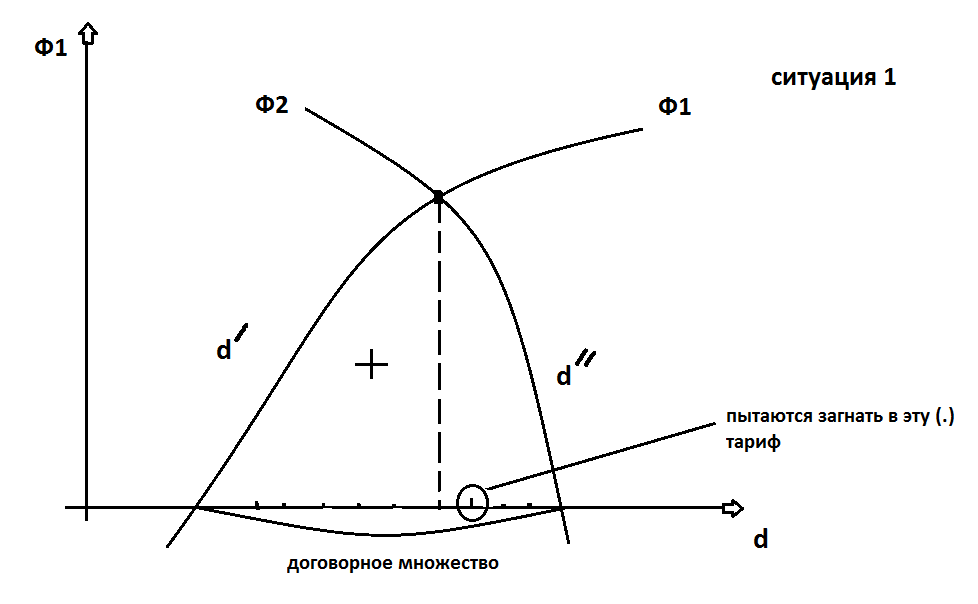
d′d′′ - и страховщик и страхователь в «плюсах».
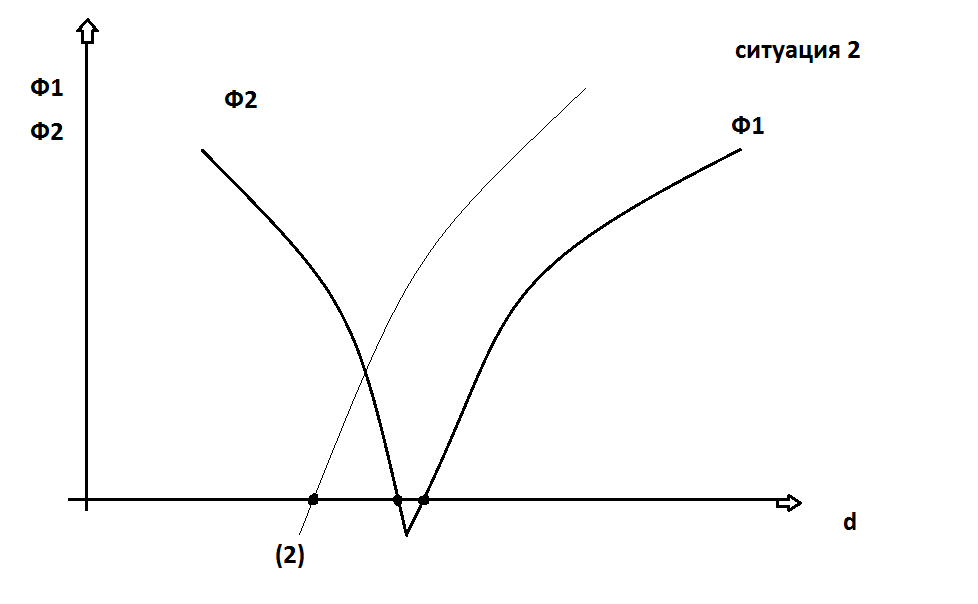
Нет выгоды в такой ситуации.
Чем >n, тем страховщик может снизить величину d, те (2)-см график.