20. Основные уравнения прямой на плоскости.

Векторное: (r₂ – r₁) N = 0, r1 – радиус-вектор начала вектора; r2 – радиус-вектор конца вектора; N – нормаль

С вектором нормали и точкой A(x-x₀)+B(y-y₀)=0; (А;В) – координаты вектора нормали, (х;у) - точки

Общее: Ах+Ву+С = 0

Каноническое: (х-х₀)/m = (y-y₀)n (m;n) – координаты направляющего вектора

Через 2 точки: (х-х₀)/(x₁-x₀) = (y-y₀)/(y₁-y₀)

Уравнение в отрезках: x/a + y/b = 1 a, b – отрезки, отсекаемые прямой на соответствующих осях

Нормальное уравнение xcosα + ycosβ – p = 0 p – расстояние от прямой до начала координат, cosα, cosβ - направляющие косинусы

Уравнение с угловым коэффициентом: y = kx+b; k=tgφ=-A/B; b = -C/B

Уравнение пучка прямых: y = y₀ + k(x-x₀)

Условие параллельности: A1/A2 = B1/B2, m1/m2 = n1/n2

Условия перпендикулярности: А1А2+В1В2 = 0; m1m2+n1n2 = 0; k1k2 = -1

Угол между прямыми: cosϴ = (A₁A₂+B₁B₂)/sqrt(A₁²+B₁²)*sqrt(A₂²+B₂²)

cosϴ = (m₁m₂+n₁n₂)/sqrt(m₁²+n₁²)*sqrt(m₂²+n₂²)

tgϴ = +-(k₁-k₂)/(1+k₁k₂)

Расстояние от точки до прямой: d = |Ax₀+Bx₀+C|/sqrt(A²+B²)

21. Канонические уравнения и определения кривых второго порядка.

Окружность – множество точек на плоскости, равноудаленных от центра (x₀;y₀) на расстояние R

(x - x₀)² + (y – y₀)² = R²

Эллипс – множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами

Гипербола – множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами

Парабола – множество всех точек плоскости, каждая из которых равноудалена от данной точки, называемой фокусом и данной прямой, называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы и обозначается через p

22 . Евклидово пространство.

Евклидово пространство – это линейное пространство, в котором каждой паре векторов x, y ставится в соответствие число, называемое скалярным произведением этих векторов. Скалярное произведение векторов удовлетворяет следующим аксиомам: (x, y, z – вектора, a - константа)

x, y --> (x, y):

(x, y) = (y, x)

(x, y+z) = (x, y) + (x, z)

(ax, ay) = a(x, y)

(x, x) >= 0

Длиной вектора в Еⁿ (евклидовом пространстве) называется число, равное |x| = √(x, x)

23. Матрица перехода из одного базиса в другой.

Пусть в пространстве Rⁿ имеется два базиса:  и  .

Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 5.1, можно линейно выразить через векторы старого базиса:

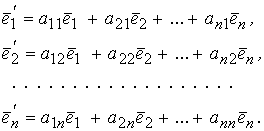(5.1)

Новые базисные векторы получаются из старых с помощью матрицы

При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица   называется матрицей перехода от базиса   к базису  .

Определитель матрицы   не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы  , были бы линейно зависимы.

Обратно, если  , то столбцы матрицы линейно независимы, и следовательно векторы  , получающиеся из базисных векторов   с помощью матрицы  , линейно независимы и значит образуют некоторый базис. Таким образом, матрицей перехода может служить любая квадратная матрица порядка n с отличным от нуля определителем.

Р ассмотрим теперь, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть   в старом базисе и   - в новом. Подставляя в последнее равенство вместо   их выражение из (5.1), получим, что

Таким образом, старые координаты вектора   получатся из новых его координат с помощью той же матрицы  , только коэффициенты соответствующих разложений образуют строки этой матрицы.