14. Скалярное, векторное и смешанное произведения векторов и их свойства.

Скалярное произведение двух векторов – это число, равное произведению их длин на косинус угла между ними.

Свойства скалярного произведения:

Выражение скалярного произведения через координаты .

Векторным произведением векторов а и b называется вектор с, который перпендикулярен векторам а и b, имеет длину, численно равную площади параллелограмма, построенного на векторах а и b, вектора а, b, с образуют правую тройку

Свойства векторного произведения:

При перестановке сомножителей векторное произведение меняет знак

k(a x b) = (ka) x b = a x (kb), где a и b – векторы, k – константа (векторное произведение обладает сочетательным свойством относительно скалярной величины)

Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору

Векторное произведение обладает распределительным свойством (a+b) x c = a x c+b x c

Выражение векторного произведения через координаты

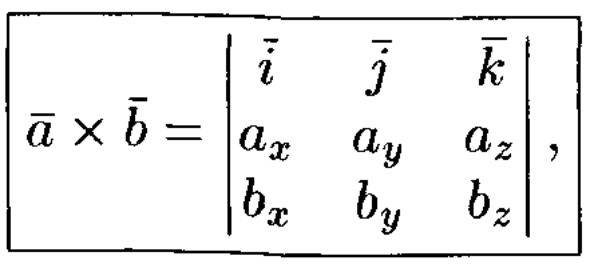
Смешанное произведение векторов а, b и с – это произведение, составленное следующим образом: (а х b) с. Первые два вектора перемножаются векторно, а их результат скалярно на третий вектор.

Смешанное произведение трех векторов – это число, равное объему параллелограмма, построенного на этих векторах, взятое со знаком «+», если они образуют правую тройку, и «-», если левую

Свойства смешанного произведения:

Смешанное произведение не меняется при циклической перестановке его сомножителей

Не меняется при перемене местами знаков векторного и скалярного умножения (а х b) с = а (b x c)

Смешанное произведение меняет знак при перестановке любых двух векторов-сомножителей

Смешанное произведение трех векторов равно нулю только тогда, когда они компланарны

Выражение смешанного произведения через координаты

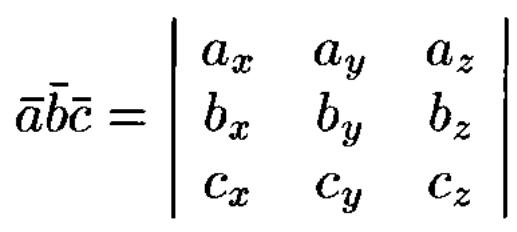
15. Линейное пространство. Определение, 8 аксиом.

Линейным пространством называется множество объектов любой природы, для которых определены 2 операции: сложения и умножения на число, причем результаты этих операций также принадлежат к данному пространству. Если операция умножения на число определена для вещественных чисел, то линейное пространство (L) называется вещественным линейным пространством, если для комплексных, то L – комплексное линейное пространство

Элементы линейного пространства называются векторами и обозначаются как обычн. векторы

Аксиомы сложения: (x, y, z - векторы)

1. x + y = y + x – коммутативность

2. (x + y) + z = x + (y + z) – ассоциативность

3. x + 0 = x , 0 – нулевой элемент (вектор)

4. для любого элемента существует противоположный элемент x + (-x) = 0

Аксиомы умножения на константу: (x, y – векторы, а, b - константы)

1. а (bx) = (ab) x – ассоциативность

2. (a+b) x = ax + bx – дистрибутивность относительно сложения констант

3. a (x+y) = ax + ay – дистрибутивность относительно сложения векторов

4. х * 1 = х

16. Линейно зависимые и линейно независимые системы векторов.

Система векторов линейно независима, если их линейная комбинация равна нулю только в том случае, когда все коэффициенты равны нулю, и линейно зависима тогда, когда линейная комбинация равна нулю, и при этом существует хотя бы 1 отличный от нуля коэффициент.