1. Определение матрицы. Сложение, вычитание матриц, умножение матрицы на число, умножение матриц, транспонирование матриц. Свойства операций над матрицами
Матрица – математический объект, имеющий вид таблицы, обозначающийся заглавными буквами, а элементы имеют двойную индексацию. Элементами могут быть буква, числа, выражения, другие матрицы. Транспонирование – замена строк на соответствующие столбцы. Выполнима всегда.
Умножение на число – каждый элемент матрицы умножается на это число. Выполнима всегда. Свойства: (a+b) A = aA +bA;
a(bA) = (ab)A = b (aA) (a, b - const)
Сложение матриц – складываются соответствующие элементы матриц. Выполнима только если матрицы имеют одинаковую разрядность. Свойства:
A + B = B + A;
(A + B) + C = A + (B + C)
A+0 = A
a(A+B) = aA + aB, a – const
Вычитание матриц А – В = А + (-В). Выполнима, если разрядность матриц совпадает
Умножение матриц происходит по правилу «строка на столбец» Складываются результаты умножения соответственных элементов i-ой строки первой матрицы и j-ого столбца второй матрицы. Выполнима, если совпадают число столбцов первой матрицы и число строк второй. Свойства:
А*В != В*А в общем случае ( равно, только если А и В – коммутирующие (перестановочные))
А(ВС) = (АВ)С
А(В+С) = АВ + АС
АЕ = А
2. Определители второго и третьего порядков. Основные свойства определителей.
Определитель – числовая характеристика квадратной матрицы. Порядок определителя совпадает с порядком матрицы
Свойства определителей:
1. Не меняется при транспонировании матриц
2. Общий множитель ряда можно вынести за знак определителя
3. При перестановке рядов определитель меняет знак
4
.
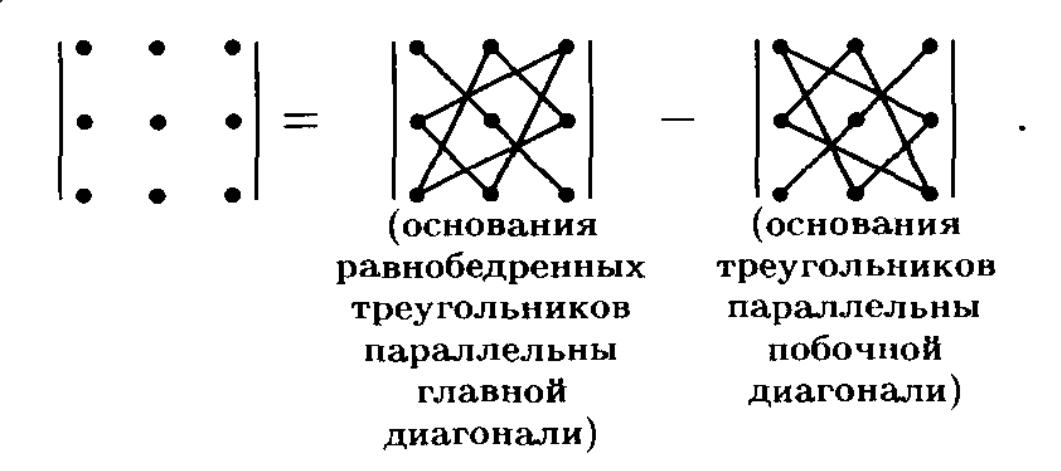Определитель равен нулю, если: 1) в нем
есть хотя бы 1 ряд, состоящий только из
нулей; 2) в нем есть хотя бы 2 одинаковых
ряда; 3) в нем есть хотя бы 2 пропорциональных
ряда
5. Определитель произведения матриц равен произведению определителей этих матриц
6. Определитель не изменится, если к ряду прибавить параллельный ряд, умноженный на число.
Вычисление определителей второго и третьего порядка:
2
Правило Саррюса
3) правило Саррюса (треугольники)
3. Алгебраические дополнения и миноры определителя n -го порядка.
Минор порядка k матрицы – определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов матрицы
Минор элемента матрицы – определитель, полученный путем вычеркивания из определителя матрицы строки и столбца, содержащих элемент, минор которого является искомым
Алгебраическое дополнение элемента – это произведение минора этого элемента и (-1) в степени суммы номеров строки и столбца, содержащих этот элемент.
4. Вычисление определителя разложением по алгебраическим дополнениям строки или столбца.
Теорема Лапласа: Определитель равен сумме попарных произведений элементов какого-либо ряда на их алгебраические дополнения. Сумма попарных произведений элементов какого-либо ряда на алгебраические дополнения элементов других рядов равна нулю
5. Вычисление определителя с помощью элементарных преобразований.
С помощью элементарных преобразований (перестановка рядов (определитель меняет знак), умножение ряда на ненулевое число, прибавление к ряду параллельного ряда, умноженного на ненулевое число) можно привести определитель к треугольному виду, в котором определитель равен произведению элементов главной диагонали
6. Определение обратной матрицы. Формула для вычисления.
Матрица В является обратной матрице А, если АВ=ВА=Е. Матрица, обратная матрице А обозначается А-1. Любая невырожденная матрица имеет обратную.
Обратная матрица – произведение единицы, деленой на определитель исходной матрицы, и союзной к исходной матрицы (алгебраические дополнения элементов, записанные в «транспонированном виде»)
7. Определение ранга матрицы.
Ранг матрицы – это наибольший порядок отличного от нуля минора данной матрицы. Например, если среди миноров третьего порядка есть ненулевые, а все миноры четвертого порядка равны нулю, то ранг матрицы равен трем.
8. Элементарные преобразования матриц. Вычисление ранга матрицы.
Элементарные преобразования матриц: перестановка рядов, умножение ряда на число, прибавление к ряду параллельного ряда, умноженного на ненулевое число, вычеркивание нулевого ряда
Ранг можно вычислить методом окаймляющих миноров (вычисление миноров, начиная с низкого порядка, пока не будет найден такой минор порядка r, у которого все окаймляющие его миноры порядка r + 1 будут равны 0 – трудоемкий метод) или с помощью элементарных преобразований путем приведения матрицы к каноническому виду (канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю), ранг канонической матрицы равен числу единиц на ее главной диагонали.
Любой минор, отличный от нуля и имеющий порядок, равный рангу матрицы, называется базисным минором