ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА

по курсу «Физика», I семестр.

1. Предмет физики. Понятие механики. Модели в механике.

Физика есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы ее движения (т.е. упорядочивание всего того, что мы называем «окружающим нас миром»).

Механика — область физики, изучающая движение материальных тел и взаимодействие между ними. Движение в механике называют изменение во времени взаимного положения тел или их частей в пространстве.

Чаще всего в механике используются две физические модели:

а) абсолютно твердое тело (в случаях, когда в условиях конкретной задачи деформацией можно пренебречь).

б) материальная точка (в случаях, когда в условиях конкретной задачи размерами тела можно пренебречь. Например, Солнце в Солнечной системе).

2. Кинематика материальной точки. Система отсчета, тело отсчета.

Кинематика точки — область кинематики, изучающая математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей тело отсчета, систему измерения положения тела в пространстве (систему координат) и прибор для измерения времени (часы).

Положение точки определяется набором обобщенных координат — упорядоченным набором числовых величин, полностью описывающих положение тела. Для описания движения практически приходится связывать с телом отсчета систему координат. В прямоугольной системе координат положение точки в пространстве задается ее проекциями на три взаимно перпендикулярные оси. Полярная система координат используется для описания положения точки на плоскости. Полярными координатами являются расстояние от полюса и угол, образованный лучом с полярной осью.

3. Путь и перемещение.

Положение точки А в пространстве можно задать с помощью радиус-вектора r, проведенного из точки отсчета О, или начала координат.

При движении материальной точки А из положения 1 в положение 2 её радиус-вектор изменяется и по величине, и по направлению, т.е. r зависит от времени t.

Геометрическое место точек концов r называется траекторией точки. Длина траектории есть путь Δs. Если точка движется по прямой, то приращение |Δr| равно пути Δs.

Пусть за время Δt точка А переместилась из точки 1 в точку 2. Вектор перемещения Δr есть приращение вектора r1 за время Δt:

Δr = r2 – r1 = (x –x0) i + (y –y0) j + (z –z0) k ;

Δr = Δx i + Δy j + Δz k;

4. Скорость.

Средний вектор скорости определяется как отношение вектора перемещения Δr ко времени Δt, за которое это перемещение произошло:

Мгновенная скорость в точке 1 равна:

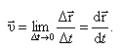
Мгновенная скорость υ – вектор скорости в данный момент времени равен первой производной от r по времени и направлен по касательной к траектории в данной точке в сторону движения точки А. Модуль вектора скорости:

При Δt → 0, т.е. на бесконечно малом участке траектории, ΔS = Δr (перемещение совпадает с траекторией). В этом случае мгновенную скорость можно выразить через скалярную величину – путь:

Таким образом вычислять скорость легче. Обратным процессом интегрированием можно вычислить путь: