Раздел 6.

1. Понятие «пространственная решетка», «элементарная ячейка», «тип решетки Браве». Примеры.

А) Пространственная решётка:

Пространственная решетка — своеобразный элемент симметрии, задающий и осуществляющий повторяемость эквивалентных точек кристаллического пространства в трех некомпланарных направлениях. Решетка как бы управляет расположением атомов в кристалле и является тем главным элементом симметрии, без которого нельзя представить строение ни одного кристалла.

Решетке подчиняется всякий бесконечный закономерный узор — одномерный, двумерный, трехмерный.

Одномерный узор-бордюр: в нём легко прослеживается линейная закономерная повторяемость, т. е. совмещение элемента с самим собой при переносе (трансляции) вдоль одного направления на величину вектора Та — трансляционного вектора.

Двумерный бесконечный узор: может быть совмещен с самим собой при переносе вдоль трансляционных векторов, лежащих в этой плоскости. Периодичность плоского узора выражается двумерной (параллелограмматической) узловой сеткой.

Трёхмерный регулярный узор: самосовмещение наступает при переносе вдоль любого трансляционного вектора; периодичность такого узора описывается трехмерной решеткой — параллелепипедальной узловой сеткой, или пространственной решеткой.

Пространственная решетка это всего лишь схема, которой подчиняется периодичность узора, не зависящая от того, какая точка узора принята за исходный узел решетки. Решетка — это своеобразный «элемент симметрии», которому могут подчиняться совершенно несхожие узоры — разные структуры кристаллов. Пространственную решетку можно считать выразителем кристаллического состояния вещества, ибо любой кристалл, даже лишенный какой-либо внешней симметрии, обладает решеткой.

Б) Элементарная ячейка (ячейка Браве):

Для выбора ячейки Браве используют три условия:

1)симметрия элементарной ячейки должна соответствовать симметрии кристалла, точнее наиболее высокой симметрии той сингонии, к которой относится кристалл. Ребра элементарной ячейки должны быть трансляциями решетки;

2)элементарная ячейка должна содержать максимально возможное число прямых углов или равных углов и равных ребер;

3)элементарная ячейка должна иметь минимальный объем.

Если ячейка удовлетворяет этим условиям, значит, она – элементарная.

В) Тип решётки Браве:

Разделяют двухмерные и трехмерные решётки Браве.

• Пять двухмерных решёток Браве

Решетка	Элементарная ячейка	Точечная группа симметрии
Косоугольная	Параллелограмм;	2
Квадратная	Квадрат;
Гексагональная	-ный ромб;
Примитивная прямоугольная	Прямоугольник;
Центрированная прямоугольная	Прямоугольник;

Обозначение   указывает на наличие двух плоскостей зеркального отражения

• Четырнадцать трехмерных решёток Браве обычно подразделяются на семь систем, в соответствии с семью различными типами элементарных ячеек: триклинной, моноклинной, ромбической, тетрагональной, кубической, тригональной и гексагональной. Каждая из систем характеризуется своим соотношением осей a,b,c и углов  .

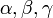Кристаллографическая система	Число ячеек в системе	Символ ячейки	Характеристики элементарной ячейки
Триклинная	1	P
Моноклинная	2	P, C
Ромбическая	4	P, C, I, F
Тетрагональная	2	P, I
Кубическая	3	P, I, F
Тригональная	1	R
Гексагональная	1	P

Примеры – увы, не понял. Какие примеры, чего примеры? Примеры всего этого?! Умереть – не встать. Сами, пущай, на экзамене придумывают. Кому надо – тот заранее озаботится