2.5. Графы со многими источниками и стоками

Алгоритм Форда-Фалкерсона примененный и для определения величины максимального потока между множеством вершин – источников и множеством вершин – стоков. Разобьем множество вершин на множество источников V₊ = {v V: Q(v) > 0}, которые образуют поток, множество стоков V_- = {v V: Q(v) < 0}, которые используют поток и множество промежуточных вершин V₀ = {v V: Q(v) = 0}, которые сохраняют поток . Преобразуем поток φ в поток, который имеет только один источник и только один сток, увеличив количество вершин в сети. Для этого добавим две новые вершины – “фиктивный” источник v_s и “фиктивный” сток v_t. Соединим вершину v_s со всеми действительными источниками. Этим дугам припишем поток, который образован соответствующим источником. А из каждого действительного стока направим дугу в “фиктивный” сток v_t. Этим дугам припишем поток, который используется соответствующим стоком. При этом пропускные способности добавленных дуг считаем бесконечными. В результате получаем сеть с одним источником и одним стоком. Применяя к ней алгоритм Форда-Фалкерсона, находим максимальный поток, который максимальный и для исходной сети.

П роиллюстирируем на примере преобразования сети с несколькими источниками и несколькими стоками до сети с одним источником и одним стоком.

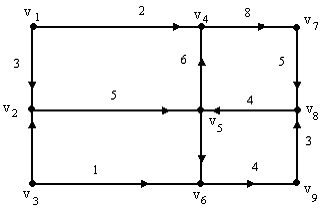
Рис. 2.5.1 Сеть с двумя стоками

На рис. 2.5.1 изображена сеть с двумя источниками v₁ и v₃ и тремя стоками v₇, v₈, v₉ Q (v₁) = 5, Q (v₃) = 3, Q (v₇) = 3, Q (v₈) = 4, Q (v₉) = 1, Q (v₂) = Q (v₄) = Q (v₅) = Q (v₆) = 0

Преобразуем эту сеть в сеть с одним источником и одним стоком.

На рис. 2.5.2 изображена сеть уже с одним источником v_s и одним стоком v_t.

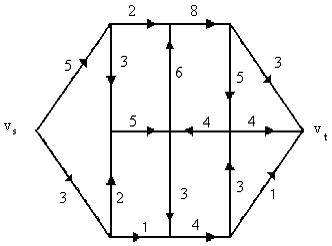
Рис. 2.5.2 Преобразованная сеть

2 .6. Задача о многополюсном максимальном потоке

Рассмотрим задачу нахождения максимального потока для всех пар узлов в неориентированной сети. Эту задачу можно рассматривать как обобщение задачи с одним источником и одним стоком, которую можно решить, применяя алгоритм Форда-Фалкерсона для каждой пары вершин. Однако более эффективным является алгоритм, предложенный Р. Гомори и Т. Ху.

Алгоритм Гомори-Ху

1. Выберем некоторые две вершины графа. Обозначим одну из них через v_s, а другую через v_t.

2. Применим алгоритм Форда-Фалкерсона и найдём максимальный поток из источника v_s в сток v_t. При этом множество помеченных вершин и множество непомеченных вершин образуют две стороны минимального разреза V_s и V_t.

3. Выберем две вершины графа v_i и v_j V_s.

4. Заменим дуги из минимального разреза (V_s, V_t) одной дугой, а вершины бока разреза, в котором не лежат вершины v_i , v_j, (например, V_t), – одной вершиной. Пропускную способность в таким образом определённой дуге примем равной пропускной способности разреза (V_s, V_t).

5. Положим: v_i = v_s, v_j = v_t и вернемся ко второму шагу. После того, как будет выбрана n - 1 пара вершин, мы определим все величин максимального потока для исходной сети. Основная идея алгоритма лежит в итеративном построении максимального остовного дерева, ветви которого соответствуют разрезам, а пропускные возможности ветвей равны пропускным способностям этих разрезов. Если бы мы применили алгоритм Форда-Фалкерсона к каждой паре вершин, то нам бы пришлось его применить раз. В алгоритме же Гомори-Ху максимальный поток между парой вершин определяется с помощью алгоритма расстановки пометок только n - 1 раз. Проиллюстрируем на примере алгоритм Гомори-Ху.

Рассмотрим сеть, изображённую на рис. 2.6.1

Рис. 2.6.1 Сеть с пропускными возможностями

Ч исла, приписанные дугам, отвечают их пропускным способностям, отвечают их пропускным способностям. Нужно для каждой пары узлов сети определить величину максимального потока между ними. Эта задача решается при n – 1= 6 – 1 = 5 итераций алгоритма Гомори-Ху. Если алгоритм Форда-Фалкерсона расстановки пометок применялся бы к каждой паре узлов, то нужно было бы решить пятнадцать задач о максимальном потоке.

Реализуем алгоритм Гомори-Ху на данной сети.

1. Выберем вершины s = v₁ и t = v₂. Минимальную пропускную способность относительно источника s = v₁ и стока t = v₂ имеет разрез со сторонами V_s = {v₁, v₃, v₄, v₅, v₆} и V_t = {v₂}. По теореме 1 величина максимального потока между вершинами v₁ и v₂ равна пропускной способности разреза (V_s, V_t): w₁₂ = w₂₁ = c(V_s, V_t) = 2 + 3 = 5. Объединим вершины с V_s в одну вершину и соединим её с вершиной v₂ веткой с пропускной способностью 5 (рис. 2.6.2).

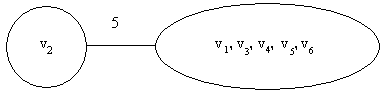
Рис. 2.6.2 Первый шаг алгоритма

2. Выберем вершины s = v₁ и t = v₃. Минимальную пропускную способность относительно источника s = v₁ и стока t = v₃ имеет разрез со сторонами V_s = {v₁} и V_t = {v₂, v₃, v₄, v₅, v₆}. По теореме 1 величина максимального потока между вершинами v₁ и v₃ равна пропускной способности разреза (V_s, V_t): w₁₃ = w₃₁ = c(V_s, V_t) = 2 + 4 + 2 = 8. Объединим вершины v₃, v₄, v₅, v₆ в одну вершину и соединим её с вершиной v₁ веткой с пропускной способностью 8 (рис. 2.6.3).

Рис 2.6.3 Второй шаг

3. Выберем вершины s = v₄ и t = v₃. Минимальную пропускную способность относительно источника s = v₄ и стока t = v₃ имеет разрез со сторонами V_s = {v₄} и V_t = {v₁, v₂, v₃, v₅, v₆}. По теореме 1 величина максимального потока между вершинами v₄ и v₃ равна пропускной способности разреза (V_s, V_t): w₄₃ = w₃₄ = c(V_s, V_t) = 2 + 5 + 4 = 11. Объединим вершины v₃, v₅, v₆ в одну вершину и соединим её с вершиной v₄ веткой с пропускной способностью 11 (рис. 2.6.4).

Рис. 2.6.4 Третий шаг

4. Выберем вершины s = v₅ и t = v₃. Минимальную пропускную способность относительно источника s = v₅ и стока t = v₃ имеет разрез со сторонами V_s = {v₅} и V_t = {v₁, v₂, v₃, v₄, v₆}. Величина максимального потока между вершинами v₅ и v₃ равна пропускной способности разреза (V_s, V_t): w₅₃ = w₃₅ = c(V_s, V_t) = 5 + 4 = 9. Объединим вершины v₃, v₆ в одну вершину и соединим её с вершиной v₅ веткой с пропускной способностью 9 (рис. 2.6.5).

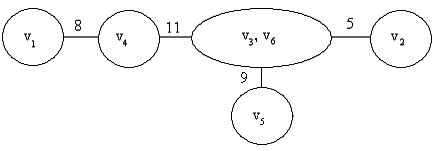
Рис. 2.6.5. Четвёртый шаг

5. Выберем вершины s = v₆ и t = v₃. Минимальную пропускную способность относительно источника s = v₆ и стока t = v₃ имеет разрез со сторонами V_s = {v₆} и V_t = {v₁, v₂, v₃, v₄, v₅}.

Рис. 2.6.6 Остаточное дерево разрезов

Величина максимального потока между вершинами v₆ и v₃ равна пропускной способности разреза (V_s, V_t): w₆₃ = w₃₆ = c(V_s, V_t) = 5 + 6 + 4 = 15. Объединим вершину v₃ с вершиной v₆ веткой с пропускной способностью 15 (рис. 2.6.6).

П о дереву перерезов, изображённого на рис. 2.6.6, легко найти остальные величины максимальных потоков. Например, v₁₆ = v₆₁ = 8, поскольку в цепи дерева разрезов, которая соединяет вершины v₁ и v₂, минимальная пропускная способность веток равна 8. Запишем величины максимальных потоков в виде матрицы:

.

Здесь на пересечение i-строки и j-столбца стоит величина максимального потока между вершинами v_i и v_j.