1 .5.2. Матрицы смежности

Матрица смежности графа – это квадратная матрица 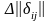, столбцам и строкам которой соответствуют вершины графа. Для неориентированного графа δ_ij равняется количеству рёбер, инцидентных i-й та j-й вершинам, для ориентированного графа этот элемент матрицы смежности соответствует количеству рёбер с началом в і-й вершине и концом в j-й. Таким образом, матрица смежности неориентированного графа симметрична (δ_ij = δ_ji), а ориентированного – необязательно. Если она всё-таки симметрична, то для каждого ребра ориентированного графа существует ребро, которое соединяет те же вершины, но направлено в противоположную сторону. Очевидно, ориентированный граф с симметричной матрицей смежности канонично соответствует неориентированному графу, который имеет ту же матрицу смежности.

Матрицы смежности рассмотренных выше графов (см. рис. 1.5.1 и 1.5.2) приведены в таблице 4.

Матрица смежности полностью определяет соответствующий неориентированный или ориентированный граф. Число его вершин равняется размерности матрицы n, i-й и j-й вершинам графа инцидентны ребер. Для неориентированного графа 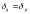, и все его ребра определяются верхним правим треугольником матрицы, расположенным над диагональю, включая последнюю.

Т аблица 4

а б

Количество их равняется сумме в этом треугольнике, то есть 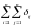. Рёбра ориентированного графа определяются всеми элементами матрицы смежности. В обоих случаях с помощью матрицы смежности легко строится, например, список ребер, который определяет граф. Элементу матрицы смежности, расположенном в і-й строке и j-м столбце, соответствует строк списка ребер (при =0 нет ни одной строки), в каждом из которых записываются номера і, j. Для неориентированного графа эти строки соответствуют только элементам названного выше верхнего правого треугольника матрицы смежности, то есть элементам с 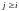, а для ориентированного графа нужно рассматривать все элементы .

И так, граф можно представить разными способами. Он может быть изображён на рисунке, задан матрицей инцидентности, списком рёбер или матрицей смежности. Графический вид зависит от формы линий и взаимного расположения вершин. Вид матриц и списка рёбер зависит от нумерации вершин и рёбер графа.

2. Потоки в сетях

2 .1. Понятие сети

Сетью будем называть ориентированный связный граф без петель и параллельных рёбер. Потоки в неориентированных графах можно изобразить в виде потоков в соответствующих ориентированных. Поток в петле не влияет на распределение потока между вершинами. Рассмотрим сеть G = (V, E), |V | = n, |E| = m. Пускай каждой дуге е_j E поставлено в соответствие неотрицательное действительное число с_j , которое назовём пропускной способностью дуги е_j. Обозначим через v_i → V множество дуг, выходящих из вершины v_i, через V → v_i – множество дуг, заходящих в вершину v_i.

Потоком в сети G из вершины v_s в вершину v_t величины w называется неотрицательная, определенная на дугах е_j, функция φ: Е → R₊ {0}, такая, что

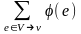– = (1)

φ(е_j) ≤ c_j, j = 1, …, m.

Вершина v_s называется источником, вершина v_t – стоком, а остальные вершины – промежуточными узлами. Число Q(v_i) = - называется чистым потоком из вершины v_i относительно φ. Число φ(е) называется потоком по дуге е. Если “реальный” поток по дуге отрицательный, то его можно сделать положительным, выбрав соответствующую ориентацию дуги e. Систему уравнений (1) можно переписать в векторном виде:

ВФ = l, (2)

где В – матрица инцидентной размерности n m, Ф = (φ(e₁) … φ(e_m))^T, l = (0..0w0..0 – w0..0)^T. Поскольку ранг матрицы инциденций равен n – 1, то система уравнений (1) избыточна: 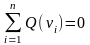. Также можно сказать, что поток φ из v_s в v_t величины w есть поток величины -w из v_t в v_s.

Пример:

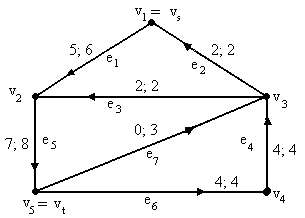
Рис. 2.1.1. Поток величины 3

С еть, изображённая на рис. 2.1.1, состоит из пяти узлов и восьми дуг. Будем рассматривать поток от v₁ до v₅. Каждой дуге приписаны два числа: первое – величина потока по дуге, второе – пропускная способность дуги. Величина этого потока равна 3. Действительно,

Q(v₁) = 5 - 2 = 3,

Q(v₂) = 7 – (5 + 2) = 0,

Q(v₃) = –4 – 0 +2 + 2 = 0, (3)

Q(v₄) = –4 + 4 = 0,

Q(v₅) = 4 + 0 – 7 = –3.

Систему уравнений (3) можно записать в векторном виде ВФ = l (2):

, , .
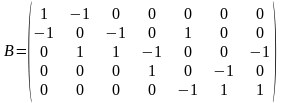
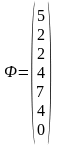