1 .4. Элементы графов

Путь – это последовательность рёбер e₁, e₂, …, e_m, такая, что рёбра e_i, e_i+1 имеют общую вершину. Число рёбер называется длинной пути. Если ни одна из вершин не появляется больше одного раза, то путь называется простым. Понятно, что в простом пути ни одно ребро не используется дважды.

Путь называется циклом, если его начальная вершина совпадает с конечной; простым циклом, если это не выполняется для других вершин.

Чередующаяся последовательность v₁, e₁, v₂, e₂, …, e_l,v_l+1 вершин и рёбер графа, такая, что e_i = v_iv_i+1 (i = 1, l), называется маршрутом. Если v₁ = v_l+1, то маршрут замкнутый, иначе открытый.

Маршрут называется цепью, если все его рёбра различны, и простой цепью, если все вершины, кроме, возможно, крайних, различны. В цепи вершины v₀ и v_k называются концами цепи. Цепь, которая соединяет вершины v_i и v_j, обозначается .

Для орграфов цепь называется путём, а цикл – контуром.

Две вершины в графе называются связными, если существует соединяющая их (простая) цепь. Граф, у которого все вершины связны, называется связным. Ориентированный граф называется сильно связным, если для любых двух вершин существует ориентированный путь, который соединяет их.

1.5. Представление графов с помощью матриц

1.5.1. Матрицы инцидентности и списки рёбер

Задать граф, значит, задать множество его вершин и рёбер, а также отношение инцидентности. Когда граф G – конечный, для описания его вершин и рёбер достаточно их занумеровать. Пускай v₁, v₂,…, v_n – вершины графа G; e₁, e₂,…, e_m – его рёбра. Отношение инцидентности можно обозначить матрицей , которая имеет m строк и n столбцов. Столбцы соответствуют вершинам графа, а строки – его рёбрам. Если ребро е_і является инцидентным вершине v_j, то , в другом случае . Это матрица инцидентности обычного графа G, являющаяся одним из способов его определения (для графа на рис. 1.5.1), она задана в табл. 2, а.

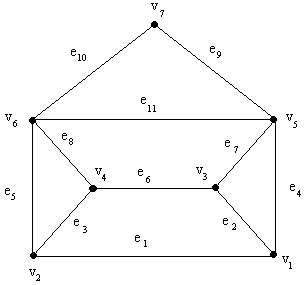
Рис. 1.5.1 Обычный граф

В матрице инцидентности ориентированного графа G, если вершина v_j – начало ребра e_i, то ; если v_j – конец e_i, то ; если e_i – петля, а v_j – инцидентная ей вершина, , где α – любое число, отличное от 1, 0 и –1, в других случаях (пример – табл. 2, б для графа рис. 1.5.2).

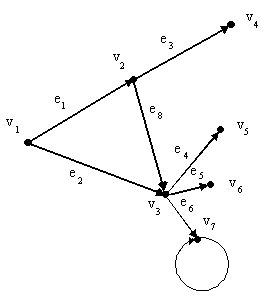
Рис. 1.5.2 Ориентированный граф

Т аблица 2

а б

В каждой строке матрицы инцидентности для неориентированного или ориентированного графа только два элемента отличны от нуля (или один, если ребро является петлёй). Потому такой способ задания графа не достаточно экономный. Отношение инцидентности можно задать ещё списком рёбер графа. Каждая строка этого списка соответствует ребру, в нём записаны номера вершин, инцидентных ему. Для неориентированного графа порядок этих вершин в строке произвольный, для ориентированного первым записывается номер или другое наименование начала ребра, а другим – его конца. В таблице 3, а и б приведены списки рёбер для графов, изображённых на рис. 1.5.1 и 1.5.2.

По списку рёбер графа можно легко определить матрицу инцидентности. Действительно, каждая строка этого списка соответствует строке матрицы с тем же номером. Для неориентированного графа в строке списка записываются номера элементов строки матрицы инцидентности, которые равняются 1, а для ориентированного графа в этой строке первым записывается номер элемента строки матрицы, который равен -1, вторым – номер элемента, который равен 1.

Таблица 3

а б