Параметрические уравнения прямой в пространстве – описание и примеры.

Мы уже выводили параметические уравнения прямой на плоскости, давайте получим параметрические уравнения прямой, которая задана в прямоугольной системе координат в трехмерном пространстве.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую a (смотрите раздел способы задания прямой в пространстве), указавнаправляющий вектор прямой   и координаты некоторой точки прямой  . От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве.

Пусть   - произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М₁, то мы получим координаты вектора  (смотрите статью нахождение координат вектора по координатам точек его конца и начала), то есть,  .

Очевидно, что множество точек   определяет прямую а тогда и только тогда, когда векторы   и   коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов   и  :  , где   - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид 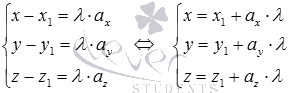  и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра  .

Приведем пример параметрических уравнений прямой в прямоугольной системе координатOxyz в пространстве: 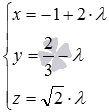 . Здесь 

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами   и  . Так как  , то по формуле для косинуса угла между векторами получим

.

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов   и  :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда   параллелен  .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:  .

Угол между прямой и плоскостью - определение.

Прежде чем говорить об определении угла между прямой и плоскостью, рекомендуем освежить в памяти понятие прямой линии в пространстве и понятие плоскости.

Чтобы определить угол между прямой и плоскостью нам потребуется несколько вспомогательных определений. Дадим эти определения.

Определение.

Прямая и плоскость пересекаются, если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости.

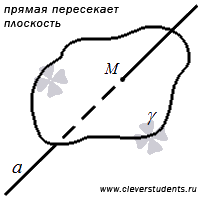
При этом прямая, которая пересекает плоскость, может быть перпендикулярна к этой плоскости.

Определение.

Прямая перпендикулярна к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

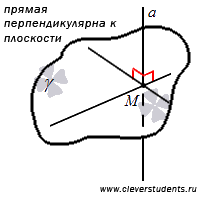
Определение.

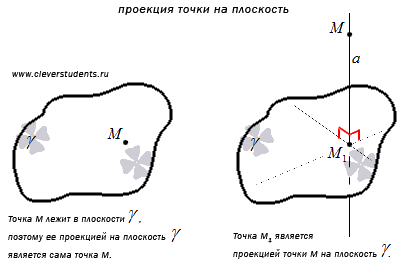
Проекцией точки М на плоскость   называется либо сама точка М, если М лежит в плоскости  , либо точка пересечения плоскости   и прямой, перпендикулярной к плоскости   и проходящей через точку М, если точка М не лежит в плоскости  .

Определение.

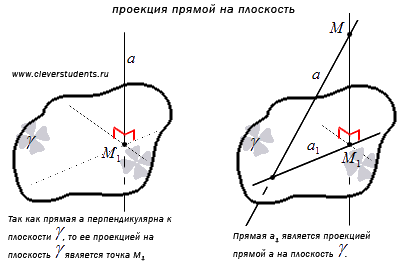
Проекцией прямой a на плоскость   называют множество проекций всех точек прямой a на плоскость  .

Очевидно, что проекцией прямой, перпендикулярной к плоскости  , на плоскость   является их точка пересечения. Также достаточно очевидно, что проекцией прямой a, которая пересекает плоскость   и не перпендикулярна к этой плоскости, на плоскость   является прямая линия, лежащая в плоскости   и проходящая через точку пересечения прямой a и плоскости  .

Теперь нам достаточно сведений, чтобы дать определение угла между прямой и плоскостью.

Определение.

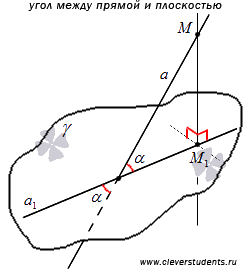
Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.

Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

Угол между перпендикулярными прямой и плоскостью считают равным  , а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным  .