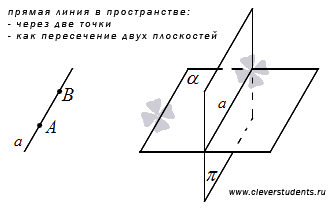
Прямая в пространстве – понятие.

В разделе прямая на плоскости мы дали представление о точке и прямой на плоскости. Прямую линию в пространстве следует представлять абсолютно аналогично: мысленно отмечаем две точки в пространстве и проводим с помощью линейки линию от одной точки до другой и за пределы точек в бесконечность.

Все обозначения точек, прямых и отрезков в пространстве аналогичны случаю на плоскости.

Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом:

• через две точки проходит единственная прямая;

• если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.

Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Направляющий вектор прямой – определение, примеры, иллюстрации.

Для правильного понимания информации этой статьи необходимо иметь четкое представление о прямой линии на плоскости и в пространстве, а также знать основные определения, связанные с векторами. Так что рекомендуем сначала ознакомиться с материалом разделовпрямая на плоскости, прямая в пространстве и векторы – основные определения.

Озвучим определение направляющего вектора прямой.

Определение.

Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.

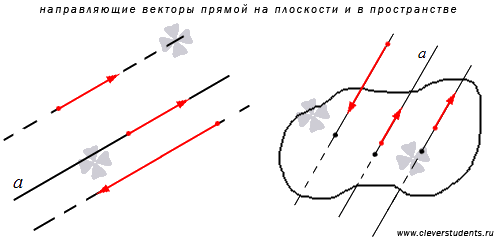
Из определения направляющего вектора прямой следует, что существует бесконечно много направляющих векторов заданной прямой. Более того все направляющие векторы прямой лежат либо на этой прямой, либо на прямой ей параллельной, то есть, все направляющие векторы заданной прямой коллинеарны. Таким образом, если   - направляющий вектор прямой a, любой из векторов   при некотором ненулевом действительном значении t также является направляющим вектором прямой a (при необходимости смотрите статью условие коллинеарности векторов).

Из определения направляющего вектора прямой также следует, что множества направляющих векторов параллельных прямых совпадают. Другими словами, если прямые a и a₁параллельны и вектор   - направляющий вектор прямой a, то вектор   также является направляющим вектором прямой a₁.

Наконец, определение направляющего вектора прямой и определение нормального вектора прямой позволяют заключить, что любой нормальный вектор прямой a перпендикулярен любому направляющему вектору прямой a.

Приведем пример направляющего вектора прямой.

Если в трехмерном пространстве введена прямоугольная система координат Oxyz, то координатные векторы   и   являются направляющими векторами координатных прямыхOx, Oy и Oz соответственно.

Канонические уравнения прямой в пространстве – описание и примеры.

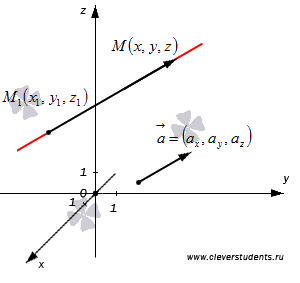
Получим канонические уравнения прямой a в трехмерном пространстве. Аналогичные действия мы проводили, когда рассматривали каноническое уравнение прямой на плоскости.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую. Выберем следующий способ задания прямой линии в пространстве: укажем точку, через которую проходит прямая a, и направляющий вектор прямой a. Будем считать, что точка   лежит на прямой а и   - направляющий вектор прямой а.

Очевидно, что множество точек   трехмерного пространства определяет прямую атогда и только тогда, когда векторы   и   коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов   и   в координатной форме. Для этого нам нужно знать координаты этих векторов. Координаты вектора   нам известны из условия. Осталось вычислить координыты вектора   - они равны разности соответствующих координат точек   и  , то есть,   (при необходимости смотрите нахождение координат вектора по координатам точек). Теперь записываем условие коллинеарности векторов   и  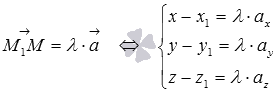: , где   - произвольное действительное число (при  точки   и   совпадают, что нас тоже устраивает).

Если  , то каждое уравнение системы 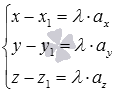  можно разрешить относительно параметра   и приравнять правые части:

Полученные уравнения вида 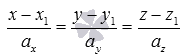  в заданной прямоугольной системе координат Oxyz определяют прямую a. Уравнения   есть канонические уравнения прямой в трехмерном пространстве в прямоугольной системе координат Oxyz. Их также называют уравнениями прямой в пространстве в каноническом виде.

Запись вида   очень удобна, поэтому ее используют даже когда одно или два из чисел   равны нулю (все три числа   одновременно не могут быть равными нулю, так как направляющий вектор   всегда ненулевой по определению). В этих случаях запись   считается условной (так как содержатся нули в знаменателях) и ее следует понимать как 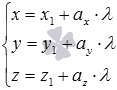 , где  . На этих частных случаях канонических уравнений прямой подробно остановимся в третьем пункте этой статьи (перейти к частным случаям канонических уравнений прямой в пространстве).

Обратите внимание на следующие важные факты:

• если известно, что прямая проходит как через точку пространства  , так и через точку 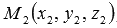 , то канонические уравнения этой прямой можно записать как  , так и  ;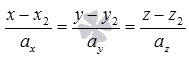

• если   - направляющий вектор прямой, то любой из векторов 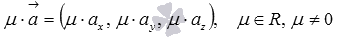  также является направляющим вектором данной прямой, следовательно, эта прямая в прямоугольной системе координат Oxyz в трехмерном пространстве может быть определена как каноническими уравнениями прямой вида  , так каноническими уравнениями прямой вида  .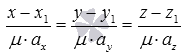

Приведем пару примеров канонических уравнений прямой в пространстве:

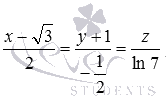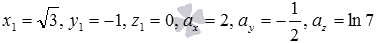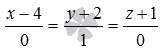• , здесь  ;

• , здесь 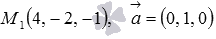 .