Геометрический смысл смешанного произведения

Геометрический смысл смешанного произведения: если тройка векторов   правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:  . В случае левой тройки   смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:  . Если  ,   и   компланарны, то их смешанное произведение равно нулю.

Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах  ,   и   равен модулю смешанного произведения этих векторов:

Объем пирамиды, построенной на этой тройке векторов равен

Свойства смешанного произведения:

1°    

2°    

3°    Три вектора компланарны тогда и только тогда, когда 

4°    Тройка векторов является правой тогда и только тогда, когда  . Если же  , то векторы  ,   и  образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

Если векторы  ,   и   заданы своими координатами, то их смешанное произведение вычисляется по формуле

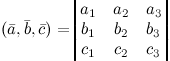
Необходимое и достаточное условие компланарности трех векторов.

Напомним определение компланарных векторов.

Определение.

Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

Два вектора   и   трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы   и   соответственно. Проведем через начало вектора   прямую b₁, параллельную прямой b, а через начало вектора  прямую a₁, праллельную прямой a. Плоскости, образуемые прямыми a и b₁, а так же прямымиb и a₁, параллельны по построению, а векторы   и   принадлежат им. Следовательно, векторы   и   компланарны.

А как же определить, являются ли три вектора компланарными?

Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.

Теорема.

Для компланарности трех векторов   и   трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Доказательство.

Пусть  , докажем что векторы   и   компланарны.

Так как 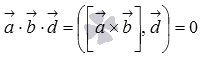 , то векторы   и   перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор   перпендикулярен и вектору   и вектору  . Следовательно, векторы   и   компланарны, так как перпендикулярны одному вектору  .

Пусть теперь векторы   и   компланарны, докажем равенство нулю смешанного произведения  .

Так как векторы   и   компланарны, то вектор   перпендикулярен каждому из них, следовательно, скалярное произведение вектора   на   равно нулю, что означает равенство нулю смешанного произведения  .

Итак, теорема полностью доказана.

Покажем применение доказанного условия компланарности трех векторов к решению задач.

Выражение смешанного произведения через координаты

Пусть заданы векторы a =а_хi +a_yj +a_zk , b =b_xi +b_yj +b_zk , с=c_xi +c_yj +c_zk . Найдем их смешанное произведение, используя выражения  в координатах для векторного и скалярного произведений:

 

Полученную формулу можно записать короче:

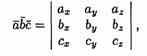
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.

Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.

Общее уравнение (полное) плоскости

где   и   — постоянные, причём   и   одновременно не равны нулю; в векторной форме:

где   — радиус-вектор точки  , вектор   перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора  :

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При   плоскость проходит через начало координат, при   (или  ,  ) П. параллельна оси   (соответственно   или  ). При   ( , или  ) плоскость параллельна плоскости   (соответственно   или  ).

Нормальный вектор плоскости - это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.

Из определения следует, что существует бесконечное множество нормальных векторов данной плоскости.

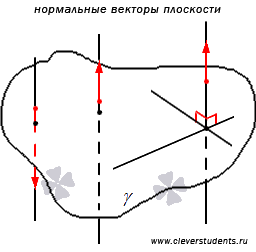
Так как все нормальные векторы заданной плоскости лежат на параллельных прямых, то все нормальные векторы плоскости коллинеарны. Другими словами, если   - нормальный вектор плоскости  , то вектор   при некотором ненулевом действительном значении t также является нормальным вектором плоскости   (смотрите статью условие коллинеарности векторов).

Также следует заметить, что любой нормальный вектор плоскости можно рассматривать какнаправляющий вектор прямой, перпендикулярной к этой плоскости.

Множества нормальных векторов параллельных плоскостей совпадают, так как прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и ко второй плоскости.

Из определения перпендикулярных плоскостей и определения нормального вектора плоскости следует, что нормальные векторы перпендикулярных плоскостей перпендикулярны.

Приведем пример нормального вектора плоскости.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Координатные векторы   являются нормальными векторами плоскостей Oyz, Oxz и Oxyсоответственно. Это действительно так, потому что векторы   ненулевые и лежат на координатных прямых Ox, Oy и Oz соответственно, которые перпендикулярны координатным плоскостям Oyz, Oxz и Oxy соответственно.

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Р ассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами   и   плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов   или  . Поэтому  . Т.к.  и  , то

.

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы   и   параллельны, а значит  .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

 или 

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно,  или  .

Таким образом,  .

Уравнение плоскости проходящей через три точки.

Пример нахождения уравнения плоскости проходящей через три точки. Данное решение является образцом работы программы, представленной на сайте. перейти к решению своей задачи Найдем уравнение плоскости проходящей через точки три заданные точки. M1 =(1,2,-2) M2 =(3,7,2) M3 = ( -2 , -1 , 1 ) Возьмем произвольную точку М ( x ,y ,z ) принадлежащую плоскости, уравнение которой нам необходимо найти. Найдем координаты следующих векторов. = ( x - ( - 2 ) , y - ( - 1 ) , z - 1 ) M3M = ( 1 - ( - 2 ) , 2 - ( - 1 ) , -2 - 1 ) = ( 3 , 3 , -3 ) M3M1 = ( 3 - ( - 2 ) , 7 - ( - 1 ) , 2 - 1 ) = ( 5 , 8 , 1 ) M3M2 Данные векторы имеют свое начало в точке M3. Очевидно, что если все четыре точки лежат в одной плоскости, то объем треугольной пирамиды, ребрами которой являются найденные векторы, равен нулю. Равенство нулю объема рассматриваемой пирамиды записывается следующим образом:   x - ( - 2 ) y - ( - 1 ) z - 1       = 0 3 3 -3 5 8 1 Представим данный определитель в виде разности двух определителей.   x - ( - 2 ) y - ( - 1 ) z - 1       = 3 3 -3 5 8 1   x y z       - 3 3 -3 5 8 1   -2 -1 1       = 3 3 -3 5 8 1 Первый определитель разлагаем по первой строке. =    ( - 1 )1+1 * x *   3 -3   8 1 +    ( - 1 )1+2 * y *   3 -3   5 1 +    ( - 1 )1+3 * z *   3 3   5 8 -      -2 -1 1       = 3 3 -3 5 8 1 =     x *   3 -3   8 1 -     y *   3 -3   5 1 +     z *   3 3   5 8 -      -2 -1 1       = 3 3 -3 5 8 1 = x * det A - y * det B + z * det C - det D = 0 det A =   3 -3   = 3 * 1 - ( -3) * 8 = 3 - ( -24) = 27 8 1 det B =   3 -3   = 3 * 1 - ( -3) * 5 = 3 - ( -15) = 18 5 1 det C =   3 3   = 3 * 8 - 3 * 5 = 24 - 15 = 9 5 8 det D =   -2 -1 1   = 3 3 -3 5 8 1 К элементам строки 2 прибавляем соответствующие элементы строки 1 , умноженные на 3.        =   -2 -1 1   = -3 0 0 5 8 1 Разлагаем определитель по элементам второй строки. = ( - 1 )2+1 * ( -3) *   -1 1   + 8 1 ( - 1 )2+2 * 0*   -2 1   + 5 1 ( - 1 )2+3 * 0*   -2 -1   = 5 8 = 3*   -1 1   = 8 1 = 3* ( ( -1) * 1 - 1 * 8 ) = = 3 * ( -9) = -27 Подставим найденные значения определителей и получим уравнение плоскости. 27 * x - 18 * y + 9 * z + 27 = 0 Разделим коэффициенты уравнения на 9 . Окончательно получим искомое уравнение плоскости. 3 * x - 2 * y + z + 3 = 0