
- •Линейная зависимость векторов
- •Компланарные векторы
- •Признак компланарности трех векторов
- •Правые и левые тройки векторов в трёхмерном пространстве
- •Свойства векторного произведения.
- •Необходимое и достаточное условие коллинеарности двух векторов.
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
- •Необходимое и достаточное условие компланарности трех векторов.
- •Прямая в пространстве – понятие.
- •Направляющий вектор прямой – определение, примеры, иллюстрации.
- •Канонические уравнения прямой в пространстве – описание и примеры.
- •Параметрические уравнения прямой в пространстве – описание и примеры.
- •Угол между прямой и плоскостью - определение.
- •Пучок плоскостей – определение.
- •Уравнение пучка плоскостей – решение задач.
- •Расстояние от точки до прямой – определение.
- •Расстояние между скрещивающимися прямыми – определение.
- •§1. Аксиоматика линейных пространств.
- •Базис и размерность линейного пространства
Свойства векторного произведения.
Так
как векторное произведение в координатах
представимо в виде определителя
матрицы 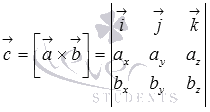 ,
то на основании свойств
определителя легко
обосновываются следующие свойства
векторного произведения:
,
то на основании свойств
определителя легко
обосновываются следующие свойства
векторного произведения:
антикоммутативность
 ;
;свойство дистрибутивности
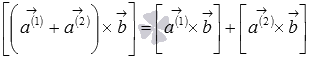 или
или 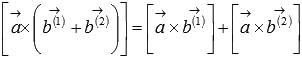 ;
;сочетательное свойство
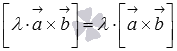 или
или 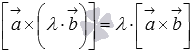 ,
где
,
где 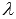 -
произвольное действительное число.
-
произвольное действительное число.
Для примера докажем свойство антикоммутативности векторного произведения.
По
определению 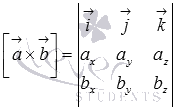 и
и 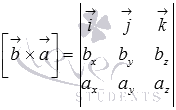 .
Нам известно, что значение определителя
матрицы изменяется на противоположное,
если переставить местами две строки,
поэтому,
.
Нам известно, что значение определителя
матрицы изменяется на противоположное,
если переставить местами две строки,
поэтому,  ,
что доказывает свойство антикоммутативности
векторного произведения.
,
что доказывает свойство антикоммутативности
векторного произведения.
Геометрический смысл векторного произведения.
По
определению длина векторного произведения
векторов равна 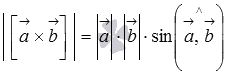 .
А из курса геометрии средней школы нам
известно, что площадь треугольника
равна половине произведения длин двух
сторон треугольника на синус угла между
ними. Следовательно, длина векторного
произведения равна удвоенной площади
треугольника, имеющего сторонами
векторы
.
А из курса геометрии средней школы нам
известно, что площадь треугольника
равна половине произведения длин двух
сторон треугольника на синус угла между
ними. Следовательно, длина векторного
произведения равна удвоенной площади
треугольника, имеющего сторонами
векторы ![]() и
и ![]() ,
если их отложить от одной точки. Другими
словами, длина
векторного произведения векторов
и
равна
площади параллелограмма со сторонами
,
если их отложить от одной точки. Другими
словами, длина
векторного произведения векторов
и
равна
площади параллелограмма со сторонами ![]() и
и ![]() и
углом между ними, равным
и
углом между ними, равным 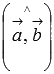 .
В этом состоит геометрический смысл
векторного произведения.
.
В этом состоит геометрический смысл
векторного произведения.
Необходимое и достаточное условие коллинеарности двух векторов.
Напомним определение коллинеарных векторов, которое было дано в статье векторы – основные определения.
Определение.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.
Это определение позволяет установить коллинеарность векторов по их изображению на плоскости с некоторой степенью точности, которая зависит от качества чертежа. Поэтому, мы нуждаемся в алгебраическом (а не в геометрическом) условии, выполнение которого будет указывать на коллинеарность двух векторов. Получим его.
Так
как операция
умножения вектора на число соответствует
сжатию или растяжению вектора при
неизменном или противоположном
направлении, то вектор ![]() ,
где
,
где ![]() -
произвольное действительное число,
коллинеарен вектору
-
произвольное действительное число,
коллинеарен вектору ![]() .
Справедливо и обратное утверждение:
если вектор
.
Справедливо и обратное утверждение:
если вектор ![]() коллинеарен
ненулевому вектору
,
то он может быть представлен в виде
коллинеарен
ненулевому вектору
,
то он может быть представлен в виде ![]() .
.
Таким
образом, мы пришли к необходимому
и достаточному условию коллинеарности
двух ненулевых векторов:
для коллинеарности двух
векторов
и
необходимо
и достаточно, чтобы они были связаны
равенствами
или ![]() .
.
Перейдем к координатной форме полученного условия коллинеарности двух векторов.
Пусть
вектор
задан
в прямоугольной
декартовой системе координат на
плоскости и имеет координаты ![]() ,
тогда вектор
имеет
координаты
,
тогда вектор
имеет
координаты ![]() (при
необходимости смотрите статью операции
над векторами в координатах).
Аналогично, если вектор
задан
в прямоугольной системе координат
трехмерного пространства как
(при
необходимости смотрите статью операции
над векторами в координатах).
Аналогично, если вектор
задан
в прямоугольной системе координат
трехмерного пространства как ![]() ,
то вектор
имеет
координаты
,
то вектор
имеет
координаты ![]() .
.
Следовательно, для
коллинеарности двух ненулевых
векторов ![]() и
и ![]() на
плоскости необходимо и достаточно,
чтобы их координаты были связаны
соотношениями:
на
плоскости необходимо и достаточно,
чтобы их координаты были связаны
соотношениями: 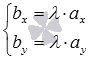 или
или 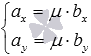 .
.
Для
коллинеарности двух ненулевых
векторов
и ![]() в
пространстве необходимо и достаточно,
чтобы
в
пространстве необходимо и достаточно,
чтобы 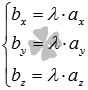 или
или 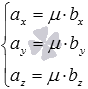 .
.
Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов и .
Если
ненулевые векторы
и
коллинеарны,
то по определению векторного произведения 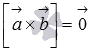 ,
что равносильно равенству
,
что равносильно равенству 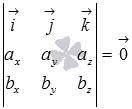 .
А последнее равенство возможно лишь
тогда, когда векторы
и
связаны
соотношениями
или
.
А последнее равенство возможно лишь
тогда, когда векторы
и
связаны
соотношениями
или ![]() ,
где
,
где ![]() -
произвольное действительное число (это
следует из теоремы
о ранге матрицы),
что указывает на коллинеарность
векторов
и
.
Таким образом, два
ненулевых вектора
и
коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору.
-
произвольное действительное число (это
следует из теоремы
о ранге матрицы),
что указывает на коллинеарность
векторов
и
.
Таким образом, два
ненулевых вектора
и
коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору.
Перейдем к применению условий коллинеарности векторов при решении примеров.
Выражение векторного произведения через координаты сомножителей
Пусть
в пространстве выбран ортонормированный
базис i , j , k . Наложим на этот базис еще
одно дополнительное условие, а именно:
из конца вектора k поворот от i к j по
кратчайшему направлению должен быть
виден против часовой стрелки.
Определение
10 . 27 Упорядоченную тройку некомпланарных
векторов![]() будем
называть правой тройкой векторов , если
из конца третьего вектора
будем
называть правой тройкой векторов , если
из конца третьего вектора![]() поворот
от первого вектора
поворот
от первого вектора ![]() ко
второму вектору
ко
второму вектору ![]() по
кратчайшему направлению виден против
часовой стрелки. Если поворот виден по
часовой стрелке, то тройку называют
левой тройкой векторов .
Оказывается, если векторы правой тройки
изменять непрерывно, но так, чтобы в
любой момент времени они были не
компланарны, то в любой момент такой
деформации эта тройка векторов будет
правой тройкой. Аналогичным свойством
обладает и левая тройка векторов. Отметим
также, что определение векторного
произведения и правой (левой) тройки
вектров связаны с наличием в пространстве
"физических" объектов: часов,
человека и т. п. В абстрактном векторном
пространстве, где такие объекты
отсутствуют, определить, какая тройка --
правая, а какая -- левая, невозможно.
Можно только все некомпланарные тройки
векторов разбить на два класса такие,
что при непрерывной деформации тройки
одного класса, при которой в любой момент
векторы тройки не компланарны, тройка
все время остается в своем классе. Итак,
пусть в трехмерном пространстве задан
ортонормированный базис i , j , k , векторы
которого образуют правую тройку векторов.
Такой базис будем называть правым .
Используя определение векторного
произведения, легко проверить следующую
таблицу умножения
по
кратчайшему направлению виден против
часовой стрелки. Если поворот виден по
часовой стрелке, то тройку называют
левой тройкой векторов .
Оказывается, если векторы правой тройки
изменять непрерывно, но так, чтобы в
любой момент времени они были не
компланарны, то в любой момент такой
деформации эта тройка векторов будет
правой тройкой. Аналогичным свойством
обладает и левая тройка векторов. Отметим
также, что определение векторного
произведения и правой (левой) тройки
вектров связаны с наличием в пространстве
"физических" объектов: часов,
человека и т. п. В абстрактном векторном
пространстве, где такие объекты
отсутствуют, определить, какая тройка --
правая, а какая -- левая, невозможно.
Можно только все некомпланарные тройки
векторов разбить на два класса такие,
что при непрерывной деформации тройки
одного класса, при которой в любой момент
векторы тройки не компланарны, тройка
все время остается в своем классе. Итак,
пусть в трехмерном пространстве задан
ортонормированный базис i , j , k , векторы
которого образуют правую тройку векторов.
Такой базис будем называть правым .
Используя определение векторного
произведения, легко проверить следующую
таблицу умножения ![]() :
a \ b i j k i 0 k - j j - k 0 i k j - i 0 Предложение
10 . 24 Пусть
:
a \ b i j k i 0 k - j j - k 0 i k j - i 0 Предложение
10 . 24 Пусть ![]() ,
, ![]() .
Тогда
.
Тогда![]() Доказательство . По
условию
Доказательство . По
условию ![]() ,
, ![]() .
В силу предложений 10.20 и 10.21
получим
.
В силу предложений 10.20 и 10.21
получим![]() (
10 .5) По тем же правилам
(
10 .5) По тем же правилам ![]() По
таблице умножения
По
таблице умножения ![]() .
Аналогично находим
.
Аналогично находим![]() ,
, ![]() .
Подставив полученные результаты в
формулу ( 10.5 ), получим
.
Подставив полученные результаты в
формулу ( 10.5 ), получим![]()
![]() Запомнить полученную формулу довольно
тяжело. Чтобы облегчить этот процесс,
введем еще два дополнительных объекта --
матрицу и определитель. Матрицей второго
порядка будем называть таблицу из
четырех чисел, которая обозначается
Запомнить полученную формулу довольно
тяжело. Чтобы облегчить этот процесс,
введем еще два дополнительных объекта --
матрицу и определитель. Матрицей второго
порядка будем называть таблицу из
четырех чисел, которая обозначается ![]() ,
матрицей третьего порядка называется
таблица из 9 чисел --
,
матрицей третьего порядка называется
таблица из 9 чисел --  Определителем
матрицы второго порядка будем называть
число
Определителем
матрицы второго порядка будем называть
число ![]() .
Определитель второго порядка
обозначается
.
Определитель второго порядка
обозначается ![]() .
Определителем матрицы третьего порядка
будем называть число
.
Определителем матрицы третьего порядка
будем называть число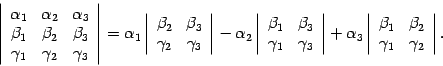 Сформулируем
словами правило вычисления определителя
третьего порядка. Берем первый элемент
первой строки. Мысленно вычеркиваем
строку и столбец с этим элементом.
Умножаем этот элемент на определитель,
оставшийся после вычеркивания. Затем
пишем знак "-" и берем второй элемент
первой строки. Мысленно вычеркиваем
строку и столбец с этим элементом и
пишем оставшийся определитель. Затем
пишем знак "+" и третий элемент
первой строки. Снова вычеркиваем строку
и столбец с этим элементом и пишем
оставшийся определитель. В дальнейшем
мы увидим, что столь сложно введенное
понятие определителя оказывается очень
полезным при решении систем линейных
уравнений, определении линейной
зависимости векторов и во многих других
задачах. Пример
10 . 1 Вычисление определителей: 1)
Сформулируем
словами правило вычисления определителя
третьего порядка. Берем первый элемент
первой строки. Мысленно вычеркиваем
строку и столбец с этим элементом.
Умножаем этот элемент на определитель,
оставшийся после вычеркивания. Затем
пишем знак "-" и берем второй элемент
первой строки. Мысленно вычеркиваем
строку и столбец с этим элементом и
пишем оставшийся определитель. Затем
пишем знак "+" и третий элемент
первой строки. Снова вычеркиваем строку
и столбец с этим элементом и пишем
оставшийся определитель. В дальнейшем
мы увидим, что столь сложно введенное
понятие определителя оказывается очень
полезным при решении систем линейных
уравнений, определении линейной
зависимости векторов и во многих других
задачах. Пример
10 . 1 Вычисление определителей: 1) 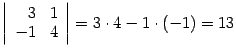 .
2)
.
2)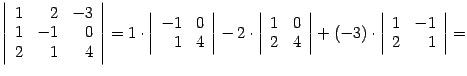
![]() .
Формула для
определителя третьего порядка позволяет
кратко записать формулу для вычисления
векторного произведения. Предложение
10 . 25 Если в правом ортонормированном
базисе i , j , k заданы координаты
векторов
,
,
то
.
Формула для
определителя третьего порядка позволяет
кратко записать формулу для вычисления
векторного произведения. Предложение
10 . 25 Если в правом ортонормированном
базисе i , j , k заданы координаты
векторов
,
,
то 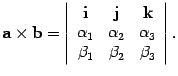 (
10 .6)
Доказательство . Достаточно
лишь написать формулу вычисления
приведенного в теореме определителя и
сравнить ее с формулой предложения
10.24 . Пример
10 . 2 Пусть
(
10 .6)
Доказательство . Достаточно
лишь написать формулу вычисления
приведенного в теореме определителя и
сравнить ее с формулой предложения
10.24 . Пример
10 . 2 Пусть ![]() ,
, ![]() .
Тогда
.
Тогда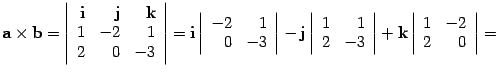
![]()
Смешанным
произведением трех векторов ![]() ,
, ![]() ,
, ![]() называется
число, равное скалярному произведению
вектора
называется
число, равное скалярному произведению
вектора ![]() на
вектор
:
на
вектор
: ![]()
