Правые и левые тройки векторов в трёхмерном пространстве

Рассмотрим упорядоченную тройку некомпланарных векторов   в трёхмерном пространстве. Совместим начала этих векторов в точке   (то есть выберем произвольно в пространстве точку   и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой  ). Концы векторов, совмещённых началами в точке  , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость   — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке  . Тогда можно в плоскости   провести через концы векторов  , совмещённых началами в точке  , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.

Упорядоченная тройка некомпланарных векторов   в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой   от плоскости  , обход концов приведённых в общее начало   векторов   в указанном порядке кажется совершающимся в плоскости   по часовой стрелке.

B противном случае   — левая тройка. В этом случае наблюдателю, находящемуся с той же стороны от плоскости  , обход концов таких векторов будет казаться совершающимся против часовой стрелки.

Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.

Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.

Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.

Правые и левые тройки некомпланарных векторов

Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями. Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки. Определение 1 :: Упорядоченная тройка некомпланарных векторов а1, а2, а3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а1 к а2 и от а2 к а3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.

Есть и ещё один способ разделить эти два класса: Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая. Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства.

ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ

ортонормированная - прямолинейная система координат в евклидовом пространстве.

Д. п. с. к. на плоскости задается двумя взаимно перпендикулярными прямыми - осями координат, на каждой из к-рых выбрано положительное направление и задан отрезок единичной длины. Точка пересечения осей координат (О)наз. началом координат. Одна из осей ( Ох )координат наз. осью абсцисс, другая - осью ординат (Оу). Оси координат делят плоскость на четыре равные области - четверти, или квадранты.

Прямоугольными декартовыми координатами точки Мназ. упорядоченная пара чисел (х, у), первое из к-рых (абсцисса) равно величине ортогональнсой проекции направленного отрезка ОМ на ось абсцисс, второе (ордината) - величине ортогональной проекции направленного отрезка ОМ на ось ординат.

Д. п. с. к. в трехмерном пространстве задается аналогично случаю плоскости: осью абсцисс, осью ординат, осью аппликат и началом координат О. Плоскости, проходящие через оси координат, наз. координатными плоскостями. Они делят пространство на 8 областей - октантов.

Иногда пользуются косоугольной (общей) декартовой системой координат, к-рая отличается от Д. п. с. к. тем, что углы между осями координат не обязательно прямые.

Векторным произведением вектора   на вектор   в пространстве   называется вектор  , удовлетворяющий следующим требованиям:

• длина вектора   равна произведению длин векторов   и   на синус угла 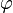  между ними:  ;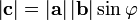

• вектор   ортогонален каждому из векторов   и  ;

• вектор   направлен так, что тройка векторов 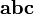  является правой;

• в случае пространства   требуется ассоциативность тройки векторов  .

Обозначение: