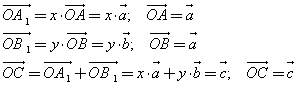Компланарные векторы

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны.

Три вектора, среди которых имеются два коллинеарных, также компланарны.

Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).

Признак компланарности трех векторов

Если вектор   можно разложить по векторам   и  , т.е. представить в виде , где х и у — некоторые числа, то векторы  ,   и  компланарны.

Необходимое условие линейной независимости системы векторов (в координатах)

Теорема (необходимое и достаточное условие линейной независимости в координатной форме). Cистема векторов   из Rⁿ линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются компоненты векторов системы:

 

 

Теорема доказана на лекции.

Следствиями из этой теоремы являются следующие утверждения:

1. если  , то система векторов   из Rⁿ — линейно зависима;

2. любая система векторов  из Rⁿ, k > n — линейно зависима.

Определение.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

 Определение. Если    - базис в пространстве и   , то числа ,  и  - называются компонентами или координатами вектора   в этом базисе.

 

В связи с этим можно записать следующие свойства:

 

-         равные векторы имеют одинаковые координаты,

 

-         при умножении вектора на число его компоненты тоже умножаются на это число,

 

=  .

 

-         при сложении векторов складываются их соответствующие компоненты.

 

;                                        ;

 +  =  .

 

Понятие ортонормированного базиса и его существование. В гл. 2 было введено понятие базиса N-мерного линейного пространства. В линейном пространстве все базисы являлись равноправными, и у нас не было оснований предпочитать один базис другому. В евклидовом пространстве существуют специальные, особо удобные базисы, называемые ортонормированными базисами . Эти базисы играют ту же роль, что и декартов прямоугольный базис в аналитической геометрии. Перейдем к определению ортонормированного базиса. Определение.Будем говорить, что п элементов электронной ₁ , ..., е _п п-мерного евклидова пространства Е образуют ортонормированный БАЗИСэтого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т . е. если

Для того чтобы установить корректность сформулированного определения, следует доказать, что входящие в это определение элементы электронной ₁ , ..., е _п образуют один из базисов рассматриваемого N-мерного пространства Е, а для этого, в силу теоремы 2.5, достаточно доказать, что эти элементы электронной ₁ , ..., е _п линейно независимы, т.е. что равенство

α ₁ электронный ₁ + α ₂ электронной ₂ + ... + α _п электронной _п = 0 (4.11)

возможно, лишь КОГДА а ₁ = α ₂ = ... = α _п = 0.  Докажем это. Пусть к - любой из номеров 1,2, ..., N. Умножая равенство (4,11) скалярно на элемент е _к и пользуясь аксиомами скалярного произведения и соотношениями (4,10), мы получим, ЧТО а _к = 0.  Докажем теперь следующую основную теорему. Теорема 4.3. Во всяком п-мерном евклидовом пространстве Е существует ортонормированный базис . Доказательство. Согласно определению размерности в пространстве Е найдется п линейно независимых элементов F ₁ , F ₂ , ..., F _п . Докажем, что можно построить п элементов электронной ₁ , е ₂ , ..., е _п , линейно выражающихся через F ₁ , F ₂ , ..., F _п и образующих ортонормированный базис (т.е. удовлетворяющих соотношениям (4.10)). Проведем доказательство возможности построения таких элементов электронной ₁ , е ₂ , ..., е _п методом математической индукции.

Если имеется только один элемент F ₁ , то для построения элемента электронной ₁ с нормой, равной единице, достаточно нормировать элемент F ₁ , т.е. умножить этот элемент на число  , обратное его норме ( н апомним, что среди линейно независимых элементов F ₁ , F ₂ , ..., F _п не может быть нулевого элемента, так что норма F ₁ больше нуля). Мы получим при этом элемент электронной ₁ =  F ₁ с нормой, равной единице.  Считая, что т - целое число, меньшее п, предположим, что нам удалось построить м элементов электронной ₁ , е ₂ , ..., е _м , линейно выражающихся через F ₁ , F ₂ , ..., F _м , попарно ортогональных и имеющих нормы, равные единице. Докажем, что к этим элементам электронной ₁ , е ₂ , ..., е _м можно присоединить еще один элемент электронной _{т +1} , линейно выражающийся через F ₁ , F ₂ , ..., F _{т +1} , ортогональный к каждому из элементов электронной ₁ , е ₂ , ..., е _м и имеющий норму, равную единице.  Убедимся в том, что этот элемент электронной _{т +1} имеет вид

электронной _{т +1}  = α _{т +1} [ е _{т +1}   - ( е _{т +1} , е _м ) , е _м - ( е _{т +1} , е _м-1 ) , е _м-1 - ... - ( е _{т +1} , е ₁ ) электронной ₁ ], (4,12)

Где а _{т +1} -. некоторое вещественное число  В самом деле, элемент электронной _{т +1} линейно выражается через F ₁ , F ₂ , ..., F _{т +1}  (в силу того, что он линейно выражается через электронную ₁ , е ₂ , ..., е _т , е _{т +1} , акаждый из элементов электронной ₁ , е ₂ , ..., е _м линейно выражается через F ₁ , F ₂ , ..., F _м ).  Отсюда сразу же следует , ЧТО ПРИ а _{т +1} ≠ 0 элемент электронной _{т +1} заведомо не является нулевым (ибо, в противном случае, являлась бы нулевым элементом некоторая линейная комбинация линейно независимых элементов F ₁ , F ₂ , ..., F _{т +1} , в которой, в силу (4,12), отличен от нуля коэффициент при е _{т +1} ).  Далее из того, что элементы электронной ₁ , е ₂ , ..., е _м попарно ортогональны и имеют нормы, равные единице, и из соотношения (4,12) сразу же вытекает, что скалярное произведение (е _{т +1} , е _К ) равно нулю для любого номера к, равного 1, 2, ..., т.  Для завершения индукции остается доказать, ЧТО число а _{т +1} можно выбрать так, что норма элемента (4,12) будет равна единице.Выше уже установлено, ЧТО ПРИ а _{т +1} ≠ 0 элемент электронной _{т +1} , а, стало быть, и элемент, заключенный в (4,12) в квадратные скобки, не является нулевым.  Стало быть, для того чтобы нормировать элемент, заключенный в квадратные скобки, следует взять число а _{т +1} обратным положительной норме этого, заключенного в квадратные скобки, элемента. При этом норма электронной _{т +1} будет равна единице.Теорема доказана.  Доказанная теорема приводит к следующему осуществляемому шаг за шагом алгоритму построения по данной системе п линейно независимых элементов F ₁ , F ₂ , ..., F _п системы п попарно ортогональных элементов электронной ₁ , е ₂ , ..., е _п , норма каждого из которых равна единице:

Указанный алгоритм обычно называют процессом ортогонализации линейно независимых элементов F ₁ , F ₂ , ..., F _п . Замечание.Конечно, в каждом п-мерном евклидовом пространстве Е существует много ортонормированных базисов. Действительно, если, например, строить ортонормированный базис процессом ортогонализации одних и тех же линейно независимых элементов F ₁ , F ₂ , ..., F _п , то, начиная процесс ортогонализации с различных элементов е _к , мы придем к различным ортонормированным базисам.Ниже, в п. 2 § 7 гл. 7 будет рассмотрен вопрос о том, как связаны между собой различные ортонормированные базисы данного евклидова пространства Е. Примером ортонормированного базиса может служить декартов прямоугольный базис евклидова пространства всех свободных векторов или совокупность п элементов 

электронной ₊₁  = (1, 0, 0, ..., 0),

электронной ₂  = (0, 1, 0, ..., 0),

_{..........................}

электронной _п  = (0, 0, 0, ..., 1)

евклидова пространства Е _п всех упорядоченных совокупностей п Ве Щ ественных чисел СО скалярным произведением (4,2). 2.Свойства ортонормированного базиса. Пусть электронной ₁ , е ₂ , ..., е _п - произвольный ортонормированный базис N-мерного евклидова про- странства Е, а х и у -. Два произвольных элемента этого пространства Найдем выражение скалярного произведения (х, у) этих элементов через их координаты относительно базиса электронной ₁ , е ₂ , ..., е _п . Обозначим координаты элементов х и у относительно базиса электронной ₁ , е ₂ , ..., е _п соответственно через (х ₁ , х ₂ ,. , .., х _п ) и (у ₁ , у ₂ , ..., у _п ), т.е. предположим, что

х = (х ₁ электронный ₁ + х ₂ электронной ₂ + ... + х _п электронной _п , у ₁ электронный ₁ + у ₂ электронной ₂ + ... + у _п электронной _п ). 

Из последнего равенства, в силу аксиом скалярного произведения и соотношений (4,10), получим 

Итак, окончательно,

(Х, у) = х ₁ у ₁ + х ₂ у ₂ + ... + х _п у _н . (4.13)

Таким образом, в ортонормированном базисе скалярное произведение двух любых элементов равно сумме произведений соответствующих координат этих элементов.  Рассмотрим теперь в п-мерном евклидовом пространстве Е совершенно произвольный (вообще говоря, не ортонормированный) базис F ₁ , F ₂ , ..., F _п и найдем выражение скалярного произведения двух произвольных элементов х и у через координаты этих элементов относительно указанного базиса.  Обозначим координаты элементов х и у относительно базиса F ₁ , F ₂ , ..., F _п соответственно через (х ₁ , х ₂ , .. ., х _п ) и (у ₁ , у ₂ , ..., у _п ), т. е. предположим, что

х = х ₁ F ₁ + х ₂ F ₂ + ... + х _н е _п    , у = у ₁ F ₁ + Y ₂ F ₂ + ... + у _п е _н .

Пользуясь аксиомами скалярного произведения, получим 

Таким образом, в произвольном базисе F ₁ , F ₂ , ..., F _п скалярное произведение двух любых элементов х = х ₁ F ₁ + х ₂ F ₂ + ... + х _н е _п , у = у ₁ е ₁ + Y ₂ F ₂ + ... + у _н е _п   определяется равенством

В котором Матрица ║ _ик ║ (г = 1, 2, ..., п, к = 1, 2, ..., п) имеет элементы _ик = (F _я , F _K ). Последнее утверждение приводит к следующему результату: для того чтобы в данном базисе F ₁ , F ₂ , ..., F _п   евклидова пространства Е скалярное произведение двух любых элементов было равно сумме произведений соответствующих координат этих элементов, необходимо и достаточно, чтобы базис F₁ , F ₂ ,. .., F _п   был ортонормированным. В самом деле, выражение (4,14) переходит в (4,13) тогда и только тогда, КОГДА Матрица ║_ик ║ с элементами _ик = (F _я , е _К ) является единичной, т. е. тогда и только тогда, когда выполнены соотношения 

устанавливающие ортонормированность базиса F ₁ , F ₂ , ..., F _п .  Вернемся к рассмотрению произвольного ортонормированного базиса электронной ₁ , е ₂ , ..., е _п п-мерного евклидова пространства Е.Выясним смысл координат произвольного элемента х относительно указанного базиса.  Обозначим координаты элемента х относительно базиса электронной ₁ , е ₂ , ..., е _п ч ерез х ₁ , х ₂ , ..., х _п , т. е. предположим, что

х = х ₁ электронный ₁ + х ₂ электронной ₂ + ... + х _п электронной _п  . (4.15)

Обозначим далее через к любой из номеров 1, 2, ..., N и умножим обе части (4,15) скалярно на элемент е _к . На основании аксиом скалярного произведения и соотношений (4,10) получим

Таким образом, координаты произвольного элемента относительно ортонормированного базиса равны скалярным произведениям этого элемента на соответствующие базисные элементы. Поскольку скалярное произведение произвольного элемента х на элемент е, имеющий норму, равную единице, естественно назвать проекцией элемента х на элемент е, то можно сказать, что координаты произвольного элемента относительно ортонормированного базиса равны проекциям этого элемента на соответствующие базисные элементы. Таким образом, произвольный ортонормированный базис обладает свойствами, вполне аналогичными свойствам декартова прямоугольного базиса