Сложение векторов

Под параллельным переносом вдоль вектора понимают перемещение всех точек пространства в одном направлении на одинаковое расстояние. Определим сложение векторов так, чтобы последовательные сдвиги вдоль двух векторов соответствовали сдвигу вдоль суммы этих векторов.

Пусть даны два вектора   и  . Приложим вектор   к некоторой точке  , получим  . Приложим вектор   к точке  , получим  . Тогда вектор   будем называтьсуммой векторов:  .

Докажем, что данное определение не зависит от выбора точки  .

Приложим вектор   к другой точке  , получим  . Приложим вектор   к точке  , получим  .

Рассмотрим направленные отрезки   и  . Они, очевидно, равны (см. рис.), поскольку   — параллелограмм.

Умножение на число

Произведением вектора   на число   называется вектор, который:

1. коллинеарен вектору  ;

2. сонаправлен ему, если 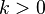 , или противоположнонаправлен, если  ;

3. длины связаны следующим соотношением:  .

Данное определение согласовано с определением сложения:

для любого натурального  .

Свойства линейных операций

Сложение векторов коммутативно:  .

Сложение векторов ассоциативно:  .

Прибавление нулевого вектора к любому не меняет последнего:  . Очевидно,  .

Для любого вектора   существует вектор   такой, что   или  .

Умножение вектора на число ассоциативно:  . Умножение вектора на число дистрибутивно относительно сложения чисел:  .

Доказательство сводится к перечислению всех возможных знаков   и  , в каждом случае утверждение очевидно.

Умножение вектора на число дистрибутивно относительно сложения векторов:  . Это следует из подобия треугольников   и   на рисунке.

Очевидно, умножение на единицу не меняет вектор:  .

Линейная зависимость векторов

ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ [vectors linear dependence] — частный случай по отношению к общему понятию линейной зависимости. Рассмотрим в качестве примера два произвольных ненулевых вектора, a иb, принадлежащих векторному пространству V.

Если можно подобрать такие не равные нулю числа α и β, что αa + βb = 0, то векторы a и b называются линейно зависимыми. Причина этого ясна: с помощью полученного равенства можно выразить, напр., вектор a через вектор b. Это значит, что a зависит от b. Можно обобщить это определение и на произвольное число векторов: если существуют такие отличные от нуля числа α₁, ..., α_n, что ∑α_ia_i = 0, то векторы называются линейно зависимыми, если же такая система чисел отсутствует, то линейно независимыми.

 

 Скалярное произведение 

     Скалярное произведение векторов   и  : 

где   - угол между векторами   и  ; если   либо  , то 

     Из определения скалярного произведения следует, что   где, например,  есть величина проекции вектора   на направление вектора  .

     Скалярный квадрат вектора: 

     Свойства скалярного произведения:             

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

М ы рассмотрели умножение вектора на число. Однако во многих задачах механики и физики встречается операция умножения вектора на вектор. Но при этом результат может быть как числом, так и вектором. Поэтому рассматривают два вида умножения векторов: скалярное и векторное.

Пусть даны два вектора   и  , угол между, которыми равен  .

Скалярным произведением векторов  и  называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается  . Итак,  .

Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.

Рассмотрим свойства скалярного произведения.

1. Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов   и    .

Очевидно, из определения скалярного произведения:

.

2. Для любого числа λ и любых векторов   имеем:

.

Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами   и   совпадает с углом между векторами   и  ,  .

Поэтому  . Откуда 

Аналогично доказывается и равенство  .

Случай λ <0 рассмотреть самостоятельно.

3. Для любых векторов   выполняется равенство  .

Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь

4. Для любого вектора   выполняется соотношение .

Действительно, так как  , то  .

Из этого свойства в частности следует  .

5. Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.

Это свойство очевидно из определения скалярного произведения.

Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.

Пример. Дан вектор  . Известно, что 

Найти  .

Имеем , т.е.  .

Найдем: 

Следовательно,  .

Р ассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора   и  .

Рассмотрим сначала все возможные скалярные произведения векторов   друг на друга.

Поэтому

Итак, скалярное произведение векторов равно сумме произведений соответствующих координат:  .

Это соотношение позволяет вычислить длину вектора через его координаты:

.

Далее из определения скалярного произведения   находим

.

Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами

.

Условие ортогональности двух векторов:

 или  .

Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.

Примеры.

1. Пусть А(-1; 1; 0), B(3; 1; -2),  . Найти:

   1. ;

   2.  и  ;

   3. .

      1. .

      2. .

      3. .

2. Найти   в  , если известны координаты его вершин A(1; 5; 6),

B (5; 3; 10), C(2; 1; 14).

3. При каком значении m векторы   и   перпендикулярны?

Условие ортогональности двух векторов  .

. Следовательно, m = 15.