4. Взаимосвязь эксперимента и модели.

Отношения между экспериментом и моделью могут выразиться: Эксперимент- источник информации для моделирования. Модель диктует, какой именно эксперимент и как нужно проводить. «Не только опыт является критерием истинности модели, но и сама постановка эксперимента диктуется моделью.»

Любой вопрос состоит из 2х составляющих-1.утверждение (препосылка впосроа), 2.вопросщающий. Предпосылка вопроса, знания, которые делают вопрос возможным. Предпосылка может быть верной, ложной или недостаточной для постановки вопроса. .эксперимент:

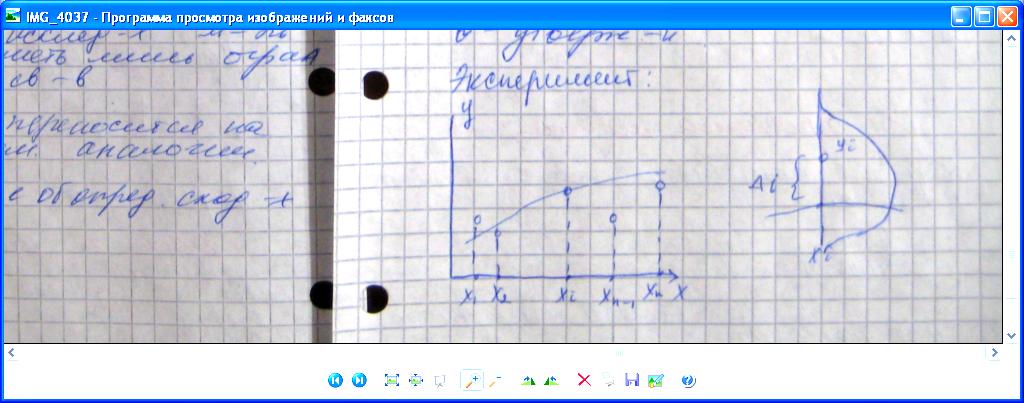
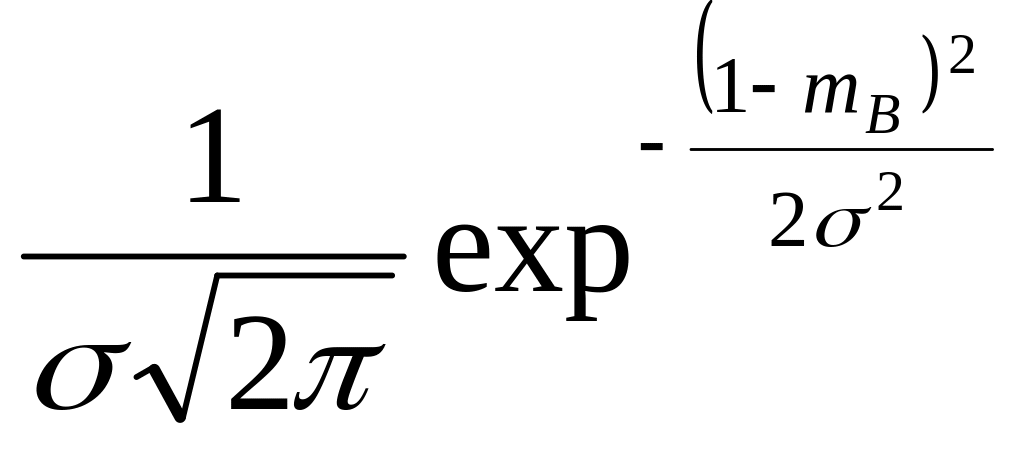
Метод максимального правободобия

-функция правдободобия.

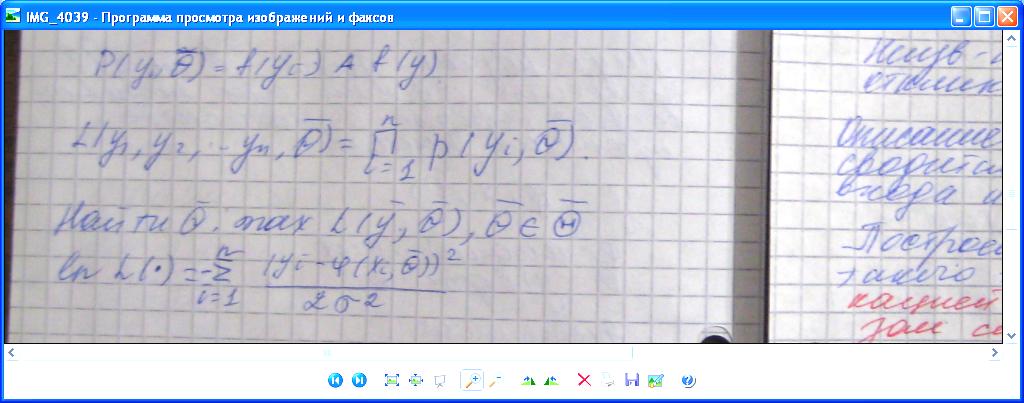
Вывод: при разных предпосылках вопрос совершенно разного комплекса по построению модели.

Экспериментальной работой занимается дисциплина «Планирование эксперимента».(при min затратах получить max результат.)\

2. Моделирование как метод научного познания.

Понятие «познание» - это отражение мозгом человека окружающего нас объективного мира. Моделирование-замещение одного объекта другим с целью получения новой информации об определенных свойствах объекта-оригинала путем изучения св-ва объекта модели. Моделирование необходимо для облегчения или упрощения познавательной деятельности, если их слишком дорого проводить на реальном объекте. Моделирование основано на способности человека абстрагировать определенные признаки и свойства различных объектов и устанавливать между ними определенные соотношения.

Модель (лат)-мера. Это созд-й человеком объект любой природы (умозрит-ой или матер-ой), кот.воспр-ит оригинал так, что изучение его природы способно дать достоверную новую информацию об оригинате. Модель отображает некот.только свойства. Ограничения:1.сущ-т лишь конечное кол-во. 2.по смыслу кажд.исслед-я м-ль и оригинал должны иметь лишь ограниченное число сходных св-в. (оригинал обладает бесконечным количеством св-в)

Результат моделирования переносится на оригинал с помощью аналогии (суждении е об определенных сходствах).

13. Методы получения равномерно распределенных случайных чисел.

При моделировании процессов и сист.исп-ся 3 вида случ.объектов. 1.сл.величины, 2.сл.события, 3.сл.процессы. Сл.величина-сл.время, сл.события-работоспос.сист. в сл.момент времени сл.события. Всегда необходима выработка случ.чисел. 1.кол-во выр-х чисел должно быть достаточно большим. Возможность создания им.модели оч.сильно зависит от наличия экон и простых способов получения чисел.

Получение случ.чисел [0,1]; (0,1); (0,1]. Способы получения. Пусть ξ€ (0,1]-равном.распр.случ.величина. x€(a,b]-любой интервал. X=a+(b-a)ξ-перераспред.

если мы хотим получить равном.распр.число, то надо взять число с вероятностью ½. Создадим случ.послед-ть z_i, z₁, z₂,…считая ее бесконечной,тогда величина, постр. В виде , будет случайным числом. Вероятность попадания сл.величины в интервал длиной ½ равна длине интервала. Раз вероятность попадания равна ½ то что нужно сгенерировать бескон.послед.сл.величин z1…zn и считать их двоичными знаками ξ. Проблема, если z_i→∞, то число тоже бесконечное, но на машине это сделать нельзя,можно ген-ть определенную конечную послед-ть. Если если комп.с k разр.сеткой,то в ней можно записать k разл.чисел с одинак.вер-ми .