10.Получение случайных чисел с произвольным законом распределения методом обратных функций

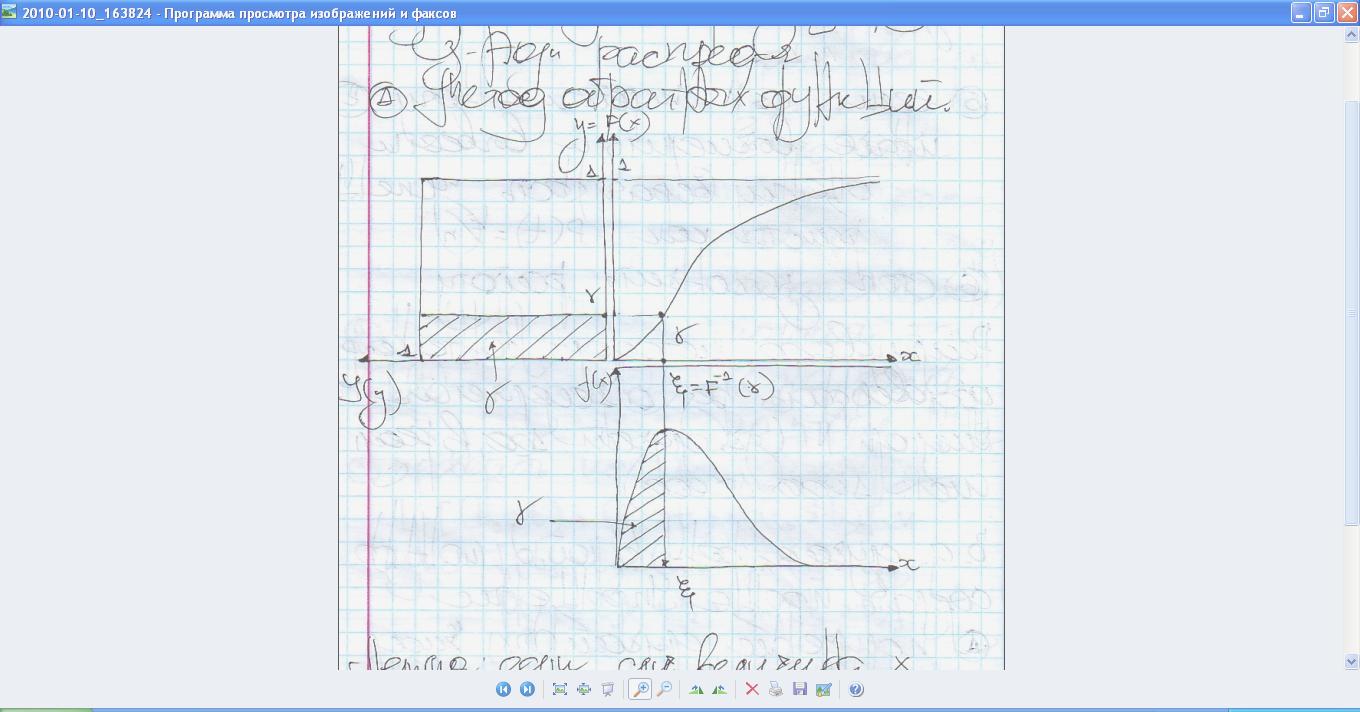
Если случ.величина x имеет плотность.распре-я f(x) и непр.ф-ю F(x), то случ.величина имеет равномерный закон на интервале y €[0,1] и . (n-1+3,3lgN). ТЕОРЕМА-Пусть F(x)-ф-я распред.некот.случ.вел x. Пусть y-случ. Величина,равномер.распред.на отрезке [0,1]. Тогда x=F^-1(y) подчин-ся законму распр-я F(x). Отсюда вытекает след.способ получения случ. Чисел, распр-х по закону F(x). с помощью (программного датчика) генератора распределения случ.чисел генер-ем величину γ и определяем другое число ξ подчин.закону F9x) по след формуле . Пример:

Дает возможность получить случайные величины для многих законов распр-я, но непригодел из-за большой трудоемкости связ.с числен-м решением задач. Поэтому используются спец.методы генерации случ.чисел на основе численных методов.

8.Классификация видов моделирования

Моделирование – замещение одного объекта другим (умозрительным или материально-реализованным) с целью получения новой информации об определенных свойствах объекта-оригинала через свойства объекта-модели.

Классификация видов моделирования:

Моделирование: 1.физическое, 2.математическое (1.аналититиское,2.компьютерное,(2.1 численное, 2.2имитационное))

Основные способы использования математических моделей таковы:

1)аналитические исследования процессов;

2)численные методы;

3)имитационное моделирование

Аналитическое моделирование

Процессы функционирования записывают в виде алгебраических, дифференциальных, интегральных и др. уравнений. Аналитическая модель в первоначальном виде мало пригодна для исследования. Может не содержать в явном виде исключающих величин. Матем. модель нужно привести к такому виду:

<искомая величина>=<конкретное аналитическое выражение>

У=exp(х² – 7х + 1)

Результат должен получиться в виде явной формулы.

Смысл аналитического моделирования – мы получаем конкретное выражение.

Результат аналитического моделирования – конкретная формула.

Сущность: нужно доказать истинность конкретной формулы. Исследование такого уравнения позволяют дать общую характеристику.

Преимущества:

- носит характер математического доказательства, это наиболее полное решение исследуемости, к которому стремимся в первую очередь.

Пренебрежение округления в пользу простоты:

используем

на самом деле

Пренебрежение малыми параметрами может привести не к той системе, не совсем точной.

Аналитическое моделирование заманчиво, но сфера применения ограничена сравнительно простыми объектами, потому что аналитическое исследование сложных объектов требует серьезных допущений и приводит к недопустимо сложным результатам (грубым).

Моделирование численными методами

Использует методы вычислительной математики и позволяет получать лишь приближенные частные решения – решения в форме:

<искомая величина>=<число>

Преимущества численного моделирования – это то, что оно позволяет решать гораздо большее число задач в отличие от математического

Недостаток: 1)дает лишь частное решение, нет обобщающего характера;

2)роль мощнейшего компьютера сводится лишь к реализации выбранного численного метода – моделируемый алгоритм в большей степени отражает именно выбранный численный метод, а не особенности модели. При смене численного метода, нужно заново разрабатывать моделируемый алгоритм.

Имитационное моделирование – это воспроизведение на компе, т.е. имитация процесса функционирования исследования системы. Характерно воспроизведение событий, происходящих в системе с сохранением их логической структуры и математическая модель к виду, разрешимому относительно искомых величин: у = ψ(х).

Имитационное моделирование совершенно аналогично экспериментальному исследованию процессов на реальном объекте, т.е. на натуре.

Имитационное моделирование – это воспроизведение на компе процессов, функции исследования системы с соблюдением логической и временной последовательности системы.

Imito –подражание, образ, копия, изображение, имитация.

Simuto – подобие, воспроизведение, моделирование, образ.

Имитационное моделирование есть полученная экспериментально инфо, к-ю нельзя получить в оригинале о сложном объекте.

Имитация есть процесс создания.

Преимущество имитационного моделирования – это возможность проигрывания различным вариантам проведения системы и ответ на вопрос, что будет если (условие); - это возможность повторения экспериментов и вероятностный характер работы модели.