9.Виды математического моделирования. Примеры

Математическое делится на аналитическое и компьютерное (численное,имитационное)

Аналитическое моделирование

Основные способы моделирования – аналитическое исследование процессов, исследование процессов при помощи числ.методов и имитац. моделирование.

При аналитическом исследовании процессов математическая модель представляется в виде математических соотношений, алгебраических, дифференциальных, интегральных матриц.

<искомая величина> = <аналитическое выражение>

Привлекательность аналитического моделирования – мы получаем результат в виде точной формулы относительно искомой величины.Благодаря им можно исследовать зависимость выхода от входных величин. Аналит.реш-наиболее полное решение, к нему стремятся больше всего. Недостатки:сложная задача для современных больших и сложных систем, чаще всего не решается (следует) специалисты идут на очень серьезное огрубление первоначальной модели (следует) получаются грубые результаты. Чаще всего на реальных объектах от аналитич.мод-я отказываются.

Численное моделирование

Используются методы численного решения задач. В результате получаем приближенное решение.

<искомая величина> = <число>

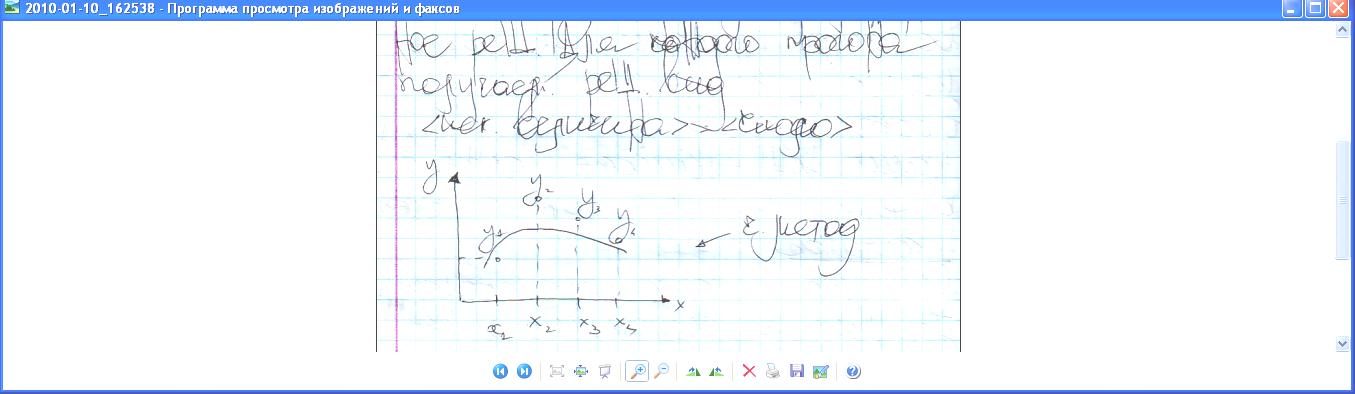
Численный метод даёт только точки.

Круг задач, решаемых численным методом, шире, чем аналитическим моделированием.

Недостатки: 1.решение задач не являетсяся полным,сводящимся к некоторому числу свод-х. 2.роль компьютера сводится к тому, что только он (числ) лишь к реализации числ.методов

Модель сложных систем не всегда удаётся привести к численному методу. Выходом является использование имитационного моделирования.

Имитационное моделирование

- воспроизведение на компьютере, т.е. имитация прос-в функционирования исследуемой системы

Для него характерно воспроизведение событий, происходящих в системе с сохранением их логической структуры и временной последовательности. Имитационное моделирование аналогично экспериментальному исследованию процессов на реальном объекте.

Imito simuto 1.подражание, копия, имитация. 2.образ, подобие, моделирование

Имитационное моделирование даёт возможность проигрывания различных вариантов поведения системы. Главное даёт ответ на вопрос «а что будет, если…?»

Требование повторяемости

Имитационный объект имеет вероятностный характер функционирования.

Имитационное моделирование – удобный инструмент для исследования случайных процессов.

При имитационном моделировании тип и структура моделируемого алгоритма обусловлено не типом управления объекта и не численными методами для их решения, а именно логической структурой и временной последовательностью.

Отказ системы происходит при отказе такой цепи

Отказал 3 и исправен 1 или 2

Вероятностью отказа 2 изделий, его приобретаем

P(t)=P_1,2(t)*P₃(t) = (1-q₁(t)*q₂(t))*(1-q₃(t)= [1 -

t – текущее время.

-переменная интегрирования.

Мы считаем, что определили функции, заданные в аналитическом виде. Это есть основа мат.модели.

Аналитическое моделирование-возможно,если интегралы берутся, т.е выражаются через элементарные ф-ии. Численное моделирование-допущений не требуется,но стадает точность вычисления.