27. Моделирование нормально распределенной случайной величины
Моделирование с норм законом –в 2 этапа. 1.получ некот.кол-во равной ξi [0,1]. 2.исп.эти числа получают псевдослуч.числа N (0,1). Три подхода к получ.нормально р.вел
1. Моделирование условий соответствия центральной пред.теореме тер.вер.
2. отслеживание сл.чисел из послед-ти ξi подг.равн.з-ну таким обр,чтобы ост.числа подг. Норм.закону.
3.прямое преобраз-е псевдослуч.числ. ξi в xi подг.нормальному з-ну.
1.кусочно-норм аппрокс, 2.многочлены спец.вида (аппрокс.полинома спец вида) –следует-легко реализ.метод обр.ф-ий. Прогр на фортране NDTRI.
Если наращивать число di=ξi- ξi-1. ТЕОРЕМА-распр.суммы одинаково распред-ся величин подчин.норм-му закону.
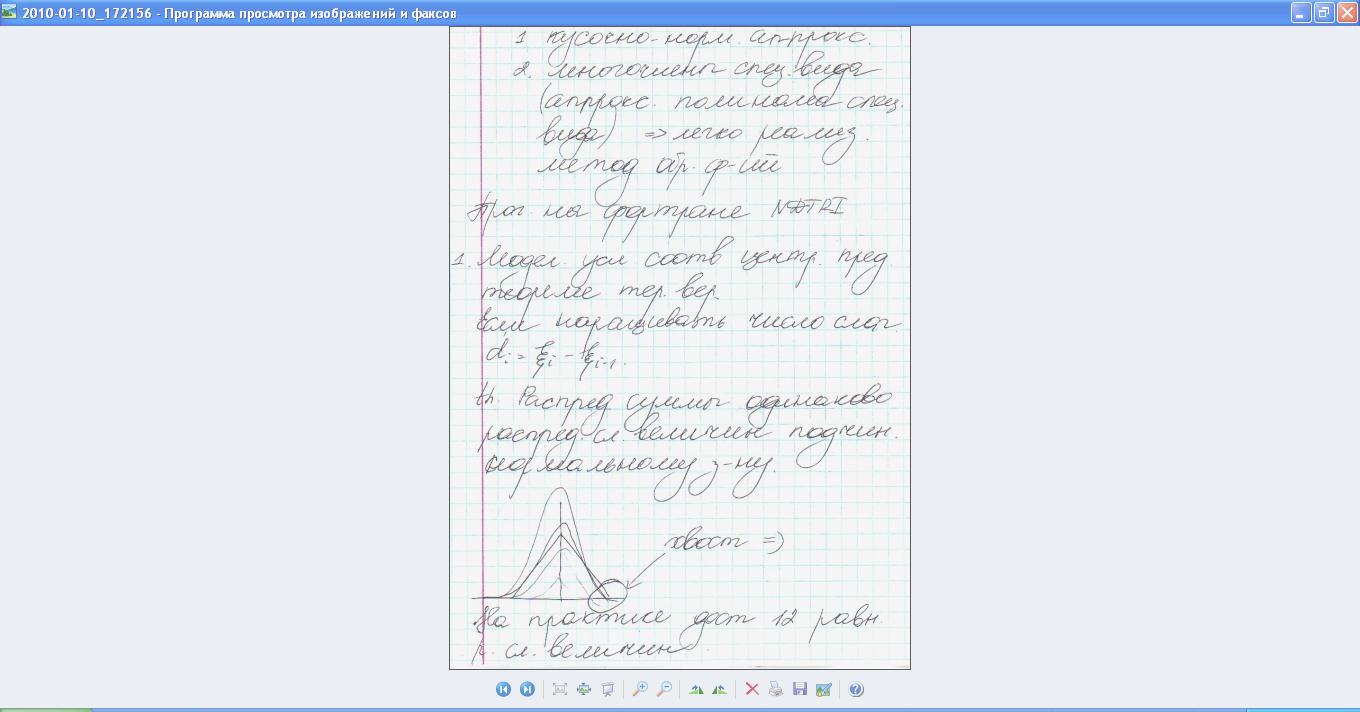
На практике дост.12 равн р.сл.величин.
-центрирование.
12(1/12)=1 дисперсия, x(m,ζ)=ζx+m
Этот метод плохо работает на хвостах.
Модификация-методТигроу.
Методы,использующие 2 подход:м\д Бокса-Маллера, м\д Морсали
Любая плосп.проход ч\з начало координат дает норм.распр. Радиус распр.по норм з-ну,а фаза распр.равномерно.
Эти формулы связаны с исп.большого кол-ва аппаратных ресурсов, Морсали предложил более простой способ.
25. Проверка независимости чисел в псевдослучайной последовательности. Критерий разностей
Сумма сл.величин если они независ др от др и распред равн на [0,1] подчинятется треугольному распр-ю.
Di=ξi-ξi-1
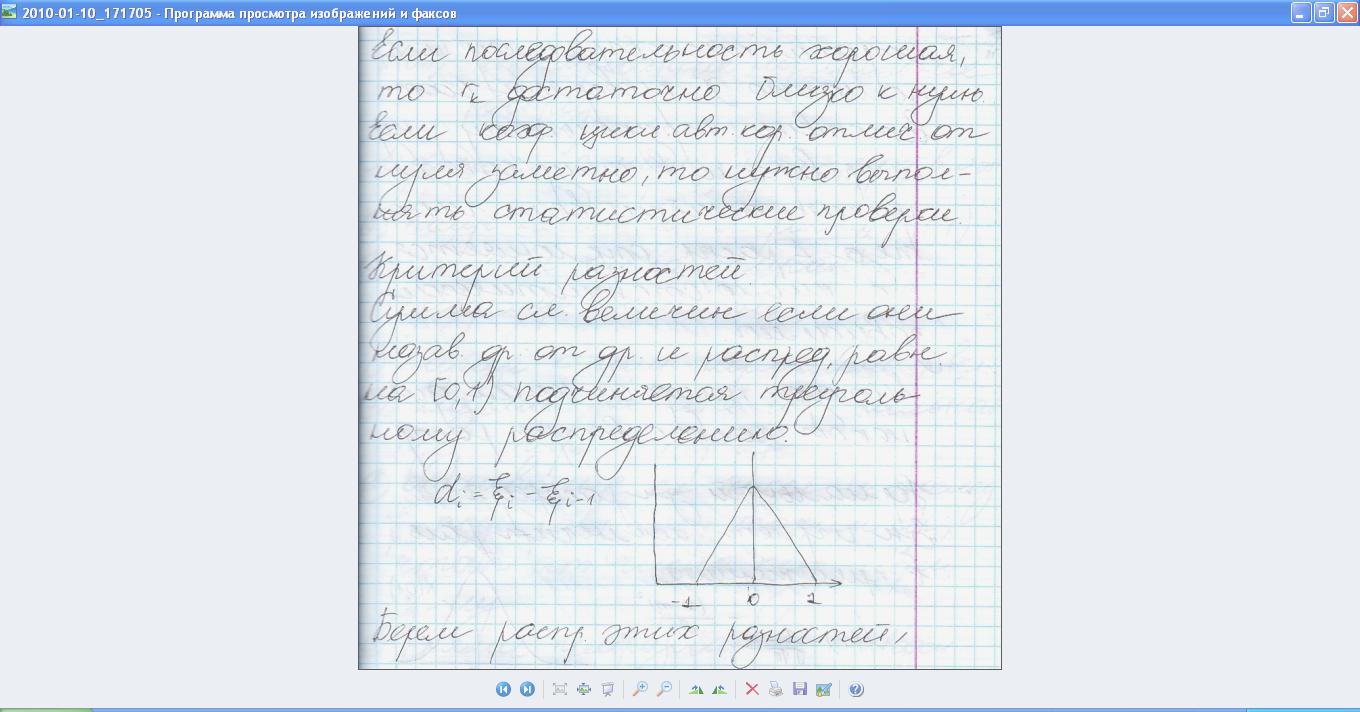
Берем распределение этих разностей, строим гистограммы и с помощью x2 проверяем соответствие треугольному знакому. Проверяем, в силу каких причин ошибки. Если гипотеза треуг распр-я отклоняется, то числа статистически независимы.
29.Распределение хи-квадрат .
Где n – число степеней свободы,
Г – гамма функция.
Моделирование распределения имеет следующие факторы:
Сумма независимых нормально распределенных по закону N(0;1) случайных величин подчиняются распределению с n степенями свободы, отсюда способ получения n независимых случ. Чисел, распределенных по закону :
Получить n нормально распределенных по закону N(0;1) чисел , i=
Частный случай:
Положим в распределении Эрланга: , можно применять формулы, характерные для распределения Эрланга.