20. Имитация случайных величин и процессов

К имитации случайных величин и процессов относят:

1.Базовый датчик- Моделирование случайных элементов в системах является одной из самых главных, базовых задач математического моделирования. Базовый датчик выдает независимые равномерно распределенные случайные величины:1 непрерывные в [0,1); 2.дискретные в Типы базовых датчиков: 1. физические (любой физический шум) – не используются, т.к. характеристики нестабильны и реализацию повторить нельзя; 2.псевдослучайные – строятся на основе детерминированного алгоритма, но полученные результаты неотличимы от случайных.

Псевдослучайные базовые датчики строятся по модели при заданном

2.Требования к базовом датчикам и проверка-

1. Отрезок апериодичности. Периодом T и длиной отрезка апериодичности датчика называются наименьшие из величин, удовлетворяющие Чем больше T и L, тем лучше датчик (особенно L).

2. Равномерность Должно быть для

3. Некоррелированность 4. Простейшие проверки

Подходят для любой непрерывной случайной величины. 1.Математическое ожидание:

2.Дисперсия:

3. Модели базовых датчиков. 1. Мультипликативный конгруэнтный метод (метод вычетов)

– множитель, M – модуль, – стартовое значение.

2. Линейные смешанные формулы.

p – порядок, стартовые значения: . Период

4. Генерация случайных событий1. Пусть имеется некоторое случайное событие А, наступающее с вероятностью р(А). Тогда ( – числа, генерируемые базовые датчики). Следовательно, генератор 1 случайного события:

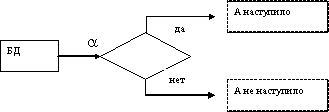
2. Полная группа попарно несовместимых событий . Пусть Идея:

,где

18. Смешанный и аддитивный конгруэнтный методы получения равномерно распределенных псевдослучайных чисел. Методы увеличения периода датчика

Смешанный метод

Сначала выбирается значение m. Чтобы получить длинный период и высокую плотность величин x_i в интервале [0, 1], величина m должна иметь большое значение. Самым удачным выбором является m=2^b, где b – число битов в слове задействованного компьютера.

Работа этих генераторов основана на использовании формулы:

x_i+1 = (a x_i + C) (mod m), .

С вычислительной точки зрения смешанный метод генерации последовательности неотрицательных целых чисел сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел. Однако экспериментальная проверка качества генерируемой последовательности чисел на основе этой формулы является сложнее.

Грин, Смит и Клем предложили аддитивный конгруэнтный метод. Он основан на использовании рекуррентной формулы

.

При X0=0 и X1=1 этот приводит к особому случаю, называемому последовательностью Фибоначчи.