Теорема: «Необходимое условие монотонности функции.»

1) Если дифференцируемая функция f(x) на множестве х возрастает, то её производная на этом множестве неотрицательна (≥0).

2) Если дифференцируемая функция f(x) на множестве х убывает, то её производная на этом множестве неположительна (≤0).

3) Если дифференцируемая функция f(x) на множестве х сохраняет постоянное значение, то её производная на этом множестве тождественно равна 0.

Док-во:

1) Пусть f(x), множестве х возрастает, т.е. f(x+∆x)>f(x), если ∆x>0 и f(x+∆x)<f(x), если ∆х<0, тогда  -всегда положительно. Перейдем к пределу при ∆х->0

, следовательно f ‘(x)≥0.

2) Если f(x) убывает, то f(x+∆x)<f(x), если ∆x>0,  f(x+∆x)<f(x), если ∆x<0       f ‘(x)≤0.

3) f(x)=c, f ‘(x)=0.

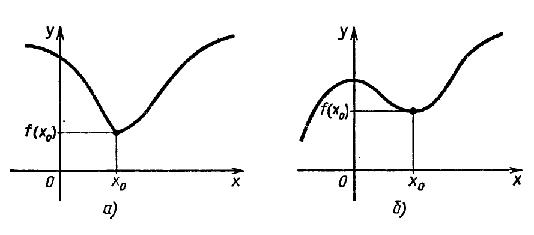
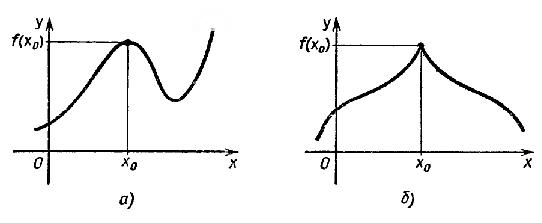
20. Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Определение. Точка x₀ называется точкой минимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≥ f(x₀.   

Определение. Точка x₀ называется точкой максимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≤ f(x₀.   

21. Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x₀экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно малых приращениях Δx имеемf(x₀+ Δx)<f(x₀), т.е.   Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x₀) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x₀) ≥ 0 а при Δx → 0 + 0 f'(x₀) ≤ 0. Так как f '(x₀) определяет число, то эти два неравенства совместны только в том случае, когда f '(x₀) = 0.

Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.

22.Первый достаточный признак экстремума.

Если производная f '(x) функции f(x) обращается в нуль в точке x₀ или не существует и при переходе через x₀ меняет свой знак, то функция f(x) имеет в этой точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если знак меняется с "-" на "+").    Доказательство. Если производная f '(x) при переходе через x = x₀ меняет знак с "+" на "-", то это означает, что при достаточно малом h производная f '(x) положительна в интервале(x₀ - h, x₀ ) и отрицательна в интервале (x₀ , x₀ + h). Следовательно, функция f(x) в интервале(x₀ - h, x₀ ) возрастает, а в интервале (x₀ , x₀ + h) убывает, то есть в точке x₀ достигает максимума.    Аналогично доказывается утверждение данной теоремы относительно минимума функции.    Заметим, что если производная f '(x), обращаясь в нуль в точке x₀, не меняет знака, то в этой точке функция не имеет экстремума, так как с обеих сторон от точки x₀ функция f(x) будет возрастать или убывать.

23. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

24. Сформулируем необходимое условие перегиба графика функции. Пусть график функции y = f(x) имеет перегиб в точке   и имеет при   непрерывную вторую производную, тогда выполняется равенство  . Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения  , в которых вторая производная равна нулю, являются абсциссами точек перегиба. Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все   из области определения функции, для которых   и  . Обычно это точки, в которых знаменатель первой производной обращается в ноль. После того как найдены все  , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции. Пусть функция y = f(x) непрерывна в точке  , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то   является точкой перегиба графика функции. Как видите первое достаточное условие не требует существования второй производной в самой точке  , но требует ее существование в окрестности точки  .

25.  Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.