1.Функция - одно из основных понятий математики, выражающее зависимость одних переменных величин от других.

Областью определения функции   (выражения f(x) ) называют множество всех значений x , для которых функция (выражение) имеет смысл.

Все значения, которые принимает функция f (x) при значениях x, принадлежащих области определения функции, образуют область значений функции, ее обозначают E (f).

График функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).

3. Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Теорема о связи бесконечно малой и бесконечно большой величиной.

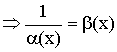Если   – бесконечно малая величина при       – бесконечно большая величина.

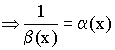Если  – бесконечно большая величина при     – бесконечно малая величина.

Доказательство:

Допустим, что   – бесконечно малая величина при  , то  , что  . Значит 

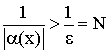
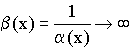
Следствие: 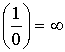  и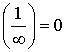 

Пусть f₁ (x)  и   f ₂ (x) бесконечно малые величины при  , т.е.        и       .

1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:

.                      (4.17)

2. Произведение бесконечно малых величин есть величина бесконечно малая:

.                           (4.18)

3. Произведение бесконечно малой величины на константу С или на функцию, имеющую конечный предел  , есть величина бесконечно малая:

.                       (4.19)

Пусть   и   бесконечно большие величины при  ,  т.е.         и      .

1. Сумма бесконечно больших величин есть величина бесконечно большая:

.                                                   (4.20)

2. Произведение бесконечно больших величин есть величина бесконечно большая:

.                                                   (4.21)

3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел  , есть величина бесконечно большая:

              

5.Экспонента — показательная функция  , где e — Число Эйлера ( ).

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

или через предел:

Здесь x — любое комплексное число.

Свойства:

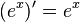• , в частности

  • Экспонента является единственным решением дифференциального уравнения 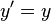  с начальными данными 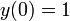 . Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.

• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.

• Экспонента является выпуклой функцией.

• Обратная функция к ней — натуральный логарифм  .

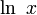• Фурье-образ экспоненты не существует

• однако преобразование Лапласа существует

• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.

• Основное функциональное свойство экспоненты, как и всякой показательной функции:

.

• Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид 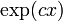 , где c — некоторая константа.

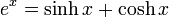•  где sinh и cosh — гиперболические синус и косинус.

6. Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Для раскрытия неопределённостей типа   используется следующий алгоритм:

1. Выявление старшей степени переменной;

2. Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа   существует следующий алгоритм:

1. Разложение на множители числителя и знаменателя;

2. Сокращение дроби.

7. 1 замечательный предел.

Возьмем круг радиуса 1, обозначим

радианную меру угла MOB через Х.

Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна

центральному углу Х, |BC| = tg x. Тогда

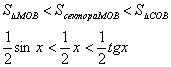
Разделим все на и получим:

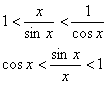
Т.к. , то по признаку существования пределов следует .

2 замечательный предел.

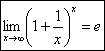
Пусть х→∞. Каждое значение х заключено между двумя положительными

целыми числами:

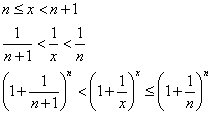
Если x→∞, то n→∞, тогда

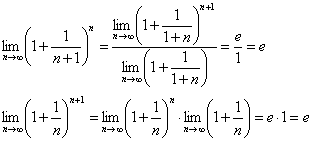
По признаку о существовании пределов:

8. Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Пусть переменная  x  стремится к  a, оставаясь больше  a, и при этом   . Тогда число  A  называют правосторонним пределом (или пределом справа) функции     и обозначают любым из символических выражений

Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае     при  x → a  со стороны меньших значений:

9. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

10.Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

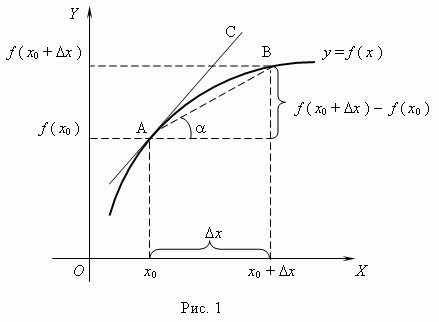
Из рис.1  видно, что для любых двух точек A и B графика функции:  

где    - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то    неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до t₀ +    точка перемещается на расстояние:  x ( t₀ +   ) - x ( t₀ ) =  , а её средняя скорость равна:  v_a =   /   . При      0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смыслпроизводной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

 

12. Теорема о производной обратной функции:

Если функция   строго монотонна на интервале   и имеет неравную нулю производную   в произвольной точке этого интервала, то обратная ей функция   также имеет производную   в соответствующей точке, определяемую равенством   или  .

Доказательство:

Рассмотрим обратную функцию  . Дадим аргументу приращение  . Ему соответствует приращение   обратной функции, причем   в силу строгой монотонности функции. Поэтому можно записать: 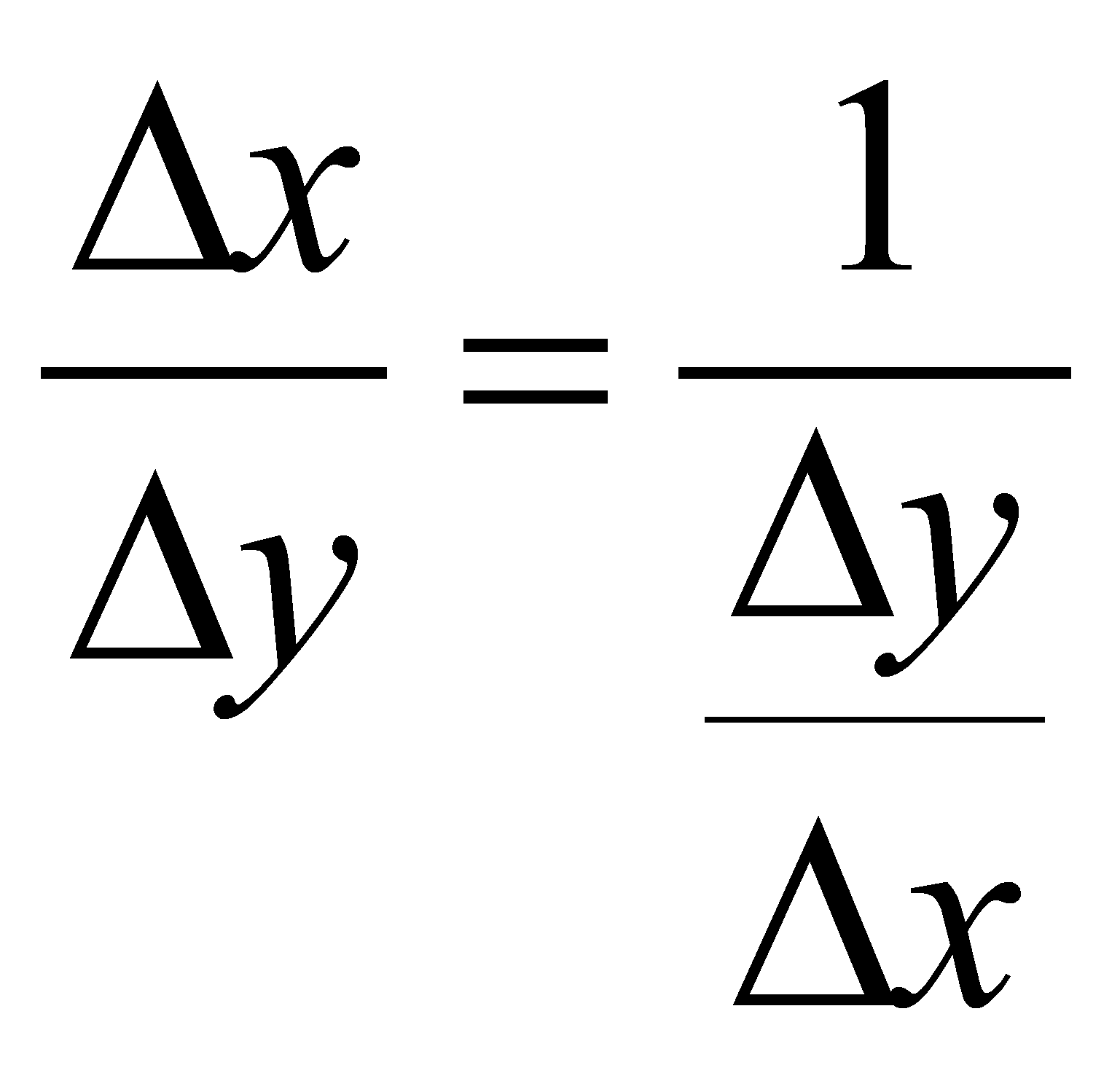 . Если  , то, в силу непрерывности обратной функции,  . И т.к. , то из   следует равенство: 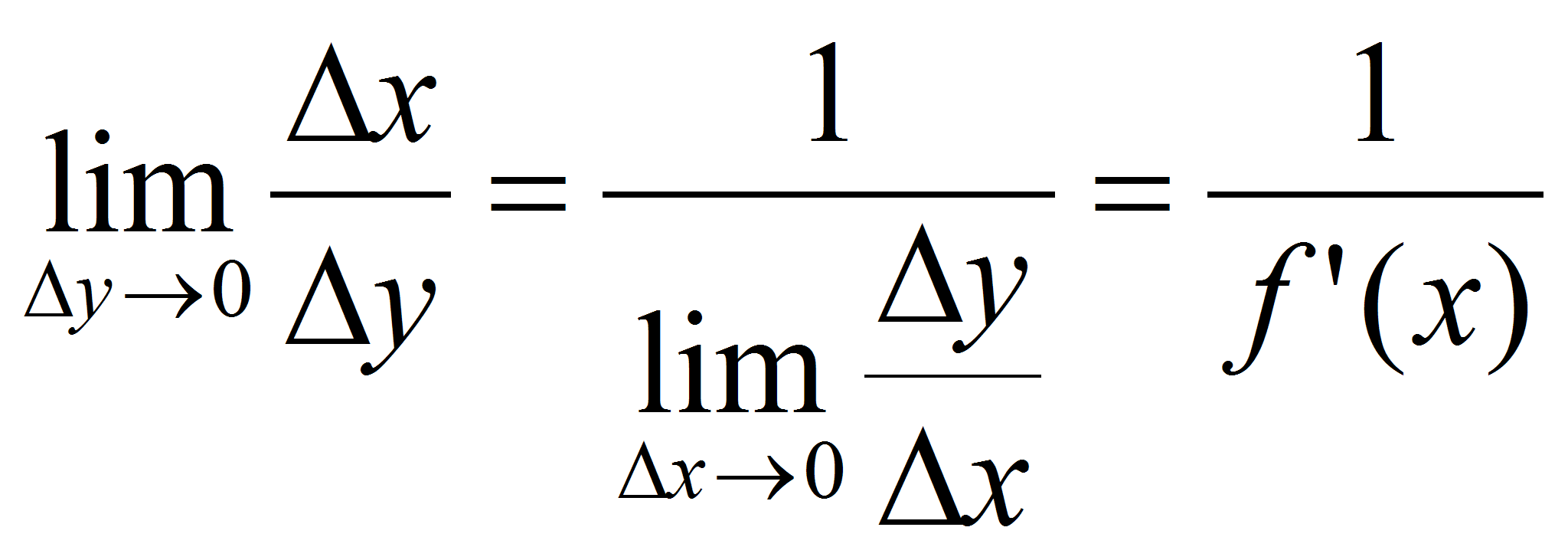 , т.е.  .

13. Теорема о производной сложной функции:

Если функция   имеет производную   в точке  , а функция   имеет производную   в соответствующей точке  , то сложная функция  имеет производную   в точке  , которая находится по формуле  .

Доказательство:

По условию  . Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем   или  , где  при  .

Функция   имеет производную в точке  :  , поэтому: , где   при  .

Подставив значение   в равенство  , получим:  ;  . Разделим полученное равенство на   и перейдя к пределу при  , получим  .

15. Дифференцирование неявных функций

Пусть уравнение   определяет   как неявную функцию от х.

а) продифференцируем по х обе части уравнения  , получим уравнение первой степени относительно  ;

б) из полученного уравнения выразим  .

Дифференцирование функций, заданных параметрически

Пусть функция задана параметрическими уравнениями  ,

тогда 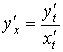 , или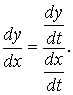 

Производная степенно-показательной функции

Данную функцию мы еще не рассматривали. Степенно-показательная функция – это  функция, у которой и степень и основание зависят от «икс». Классический пример, который вам приведут в любом учебнике или на любой лекции:

Как найти производную от степенно-показательной функции?

Необходимо использовать только что рассмотренный приём – логарифмическую производную. Навешиваем логарифмы на обе части:

Как правило, в правой части из-под логарифма выносится степень:

В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле  .

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

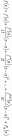Окончательно: 

16. Производная от производной у' функции у называется второй производной этой   функции и обозначается у" или f"(х):

y" = (y')';     f"(х) = [ f(х)]'.

Производные высших порядков (вторая, третья и т. д.) вычисляются последовательным дифференцированием данной функции.

Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.

, где R_n(x) - остаточный член формулы Тейлора.

19. Необходимое и достаточное условие постоянства функции на промежутке

Теорема Пусть функция f(x) определена в промежутке X и имеет внутри него конечную производную f/(x) , а на концах (если они принадлежат X) сохраняет непрерывность. Для того чтобы f(x) была в X постоянной, достаточно условие f/(x)=0  внутри X. Доказательство Пусть это условие выполнено. Фиксируем некоторую точку x0 из промежутка X и возьмем любую другую его точку x. Для промежутка [х0,х]  или [х,х0]  удовлетворены все условия теоремы Лагранжа. Следовательно, можем написать

f(x)−f(x0)=f/(c)(x−x0), 

где c содержится между x0 и x, а значит, заведомо лежит внутри X. Но, по предположению, f/(c)=0 , так что для всех x из X

f(x)=f(x0)=const.

Теорема доказана.