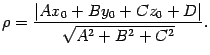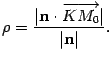1.Вектор — направленный отрезок. Обозначения:  Длиной (модулем) вектора   называется длина отрезка AB. Коллинеа́рность — отношение параллельности векторов: два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допусти́м синоним — «параллельные» векторы. Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

2.Произведением вектора   на число λ называется вектор   . Направление вектора  , при   совпадает с направлением вектора   , если λ > 0, и противоположно этому вектору, если λ < 0.

Умножение вектора на число

Свойства умножения

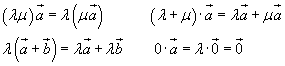
3. Суммой двух векторов   и   называется вектор   с координатами   . Для любых векторов справедливы равенства:

• 

• 

• 

Каковы бы ни были три точки A, B и C, имеет место векторное равенство   . Отсюда следует правило параллелограмма:

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Разностью двух векторов   и   называют такой вектор   , который в сумме с вектором   дает вектор   .

6.Если линейная комбинация   может представлять собой нулевой вектор тогда, когда среди чисел   есть хотя бы одно, отличное от нуля, то система векторов   называется линейно зависимой.

Если линейная комбинация   представляет собой нулевой вектор только тогда, когда все числа   равны нулю, то система векторов   называется линейно независимой.

7. ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т- прямолинейная система координат на плоскости или в пространстве.

Координатами вектора называются коэффициенты его разложения по базисным векторам.

Координаты же вектора – это его разложение по базису  , в данном случае  . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости  .

8.

9.

10. Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов   и   будем обозначать как  . Тогда формула для вычисления скалярного произведения имеет вид 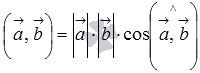 , где   и  - длины векторов   и   соответственно, а 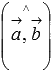  - угол между векторами   и  .

Для любых векторов   и   справедливы следующие свойства скалярного произведения:

15.Смешанным произведением трех векторов   и   называется действительное число, равное скалярному произведению векторов   и  , где   - векторное произведение векторов   и  .

Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

Объём параллелепипеда, построенного на векторах  , равен модулю смешанного произведения данных векторов.

Объем пирамиды (объем тетраэдра) построенной на векторах a, b и c равен шестой части модуля смешаного произведения векторов составляющих пирамиду:

V = 1 |a·[b × c]|

6

21. Определение. Если заданы две прямые y = k₁x + b₁,  y = k₂x + b₂, то острый угол между этими прямыми будет определяться как

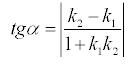
Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂.

            Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА,  В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

            Координаты точки пересечения двух прямых находятся как решение системы  уравнений этих прямых.

28. Пусть плоскость задана уравнением и дана точка . Тогда расстояние от точки до плоскости определяется по формуле

(11.7)

        Доказательство.     Расстояние от точки   до плоскости   -- это, по определению, длина перпендикуляра   , опущенного из точки   на плоскость   (рис. 11.9).

Рис.11.9.Расстояние от точки до плоскости

Вектор   и нормальный вектор n плоскости   параллельны, то есть угол   между ними равен 0 или   , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

(11.8)

Координаты точки   , которые нам неизвестны, обозначим   . Тогда   . Так как   , то   . Раскрыв скобки и перегруппировав слагаемые, получим

(11.9)

Точка   лежит на плоскости   , поэтому ее координаты удовлетворяют уравнению плоскости:   . Отсюда находим, что   . Подставив полученный результат в формулу (11.9), получим   . Так как   , то из формулы (11.8) следует формула (11.7). 

23. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

     (10)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0.     

22. Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.

Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M1, не лежащая на прямой a. Проведем через точку M1 прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H1. Отрезок M1H1 называется перпендикуляром, проведенным из точки M1 к прямой a.

Если мы определим координаты   точки H₁, то искомое расстояние   мы сможем вычислить, используя формулу для нахождения расстояния от точки M₁ до точки H₁ по их координатам:  .

Осталось разобраться с нахождением координат точки H₁.

Мы знаем, что прямой линии в прямоугольной системе координат Oxy соответствует некотороеуравнение прямой на плоскости. Будем считать, что способ задания прямой a в условии задачи позволяет написать общее уравнение прямой a или уравнение прямой с угловым коэффициентом. После этого мы можем составить уравнение прямой, проходящей через заданную точку M₁ перпендикулярно заданной прямой a. Обозначим эту прямую буквой b. Тогда точка H₁ – это точка пересечения прямых a и b, следовательно, координаты точки H₁можно определить, обратившись к материалу статьи координаты точки пересечения двух прямых.

Итак, мы получили алгоритм для нахождения расстояния от заданной точки  до заданной прямой a:

• находим общее уравнение прямой a вида 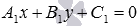  или уравнение прямойa с угловым коэффициентом  ;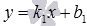

• получаем общее уравнение прямой b вида 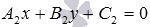  или уравнение прямой b с угловым коэффициентом вида 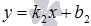 , учитывая, что прямая bпроходит через заданную точку M₁ и перпендикулярна заданной прямой a;

• определяем координаты   точки H₁ - точки пересечения прямых a и b, решая систему линейных уравнени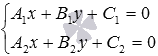й   или  ;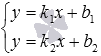

• вычисляем требуемое расстояние от точки M₁ до прямой a по формуле  .