
- •Часть1. Теплообмен излучением Основные преставления о тепловом излучении Законы теплового излучения
- •Угловые коэффициенты
- •Типовая задача
- •Теплообмен между двумя элементарными площадками
- •Теплообмен между двумя плоскими стенками с диатермической средой
- •Теплообмен излучением между тремя плоскопараллельными поверхностями (терморадиационный экран)
- •Теплообмен излучением между двумя плоскими поверхностями бесконечной протяженности между которыми помещены несколько экранов
- •Случай в замкнутой полости
- •Часть 2. Теплообмен излучением в излучающе-поглощающей среде Особенности излучения и поглощения газов
- •Основной закон переноса лучистой энергии в излучающе-поглощающей среде
- •Собственное излучение газового объема
- •Теплообмен излучением
Теплообмен между двумя элементарными площадками
Найдем энергию, падающую за одну секунду на вторую площадку из той энергии, которую излучает первая площадка:

Поток лучистой энергии от второй площадки к первой

Фактическое количество энергии переданное первым элементом второму найдется путем вычитания
![]()
Проинтегрировав последнее выражение, найдем:
![]()
Воспользовавшись формулой для углового коэффициента, преобразуем последнее выражение к виду:
![]() ,
,
где
![]()
Нами принималось. что излучение со стороны первой площадки обязательно попадает на какую-либо площадку второго тела. Поэтому последняя формула записывается в виде:
![]()
где S0 - расчетная площадь.
Энергия падающая на первую площадку со стороны второй за одну секунду равна
![]()
где
![]()
Теплообмен между двумя плоскими стенками с диатермической средой
Диатермической средой (например газы при не слишком больших температурах) называется среда слабо поглощающая тепловое излучение (коэффициент поглощения практически равен нулю).
Пусть имеются две параллельные поверхности с заданными температурами и поглощательными способностями. В данном случае наблюдается сложный процесс многократных постепенно затухающих поглощений и отражений луча. При этом часть энергии будет возвращена на первоисточник, тормозя процесс теплообмена. В соответствии с рисунком первая поверхность излучает E1 . Из этого количества вторая поверхность поглощает E1a2 и отражает в сторону поверхности F1
E1 = (1 - a2 )
Причем из этого количества первая поверхность поглощает
E1 (1 - а2) а1
и отражает
E1 (1- а2 ) (1- а1 )
Вторая поверхность вновь поглощает
E1 (1- а2 ) (1- а1 ) а2
и отражает
E1 (1- а2 )2 (1- а1 )
и т.д.
Чтобы найти энергию q12 , которую первая поверхность путем лучеиспускания передает второй, надо из первоначально испускаемой энергии вычесть то, что возвращается и снова поглощается, и ту энергию, которая поглощается от излучения второй поверхности. первое слагаемое получается путем суммирования выражений выше
![]()
где
![]()
Но так как p<1, то сумма бесконечно убывающей геометрической прогрессии в скобках будет равна
![]()
Следовательно, искомая сумма равна
![]()
Аналогично находится вторая сумма
![]()
Суммируя все три суммы, получим:
![]()
Учитывая, что
![]() и
и
![]()
где C0 =5.668 Вт/(м2К4), найдем итоговою формулу:
 ,
Вт/м2
,
Вт/м2
где

приведенная степень черноты системы.
С
учетом того, что
![]() ,
в иной форме можно записать
,
в иной форме можно записать

Теплообмен излучением между тремя плоскопараллельными поверхностями (терморадиационный экран)
Имеем лучистый
теплообмен между двумя плоскопараллельными
пластинами. Между ними расположена
экранирующая пластина. Примем
![]() .
.
При отсутствии экрана
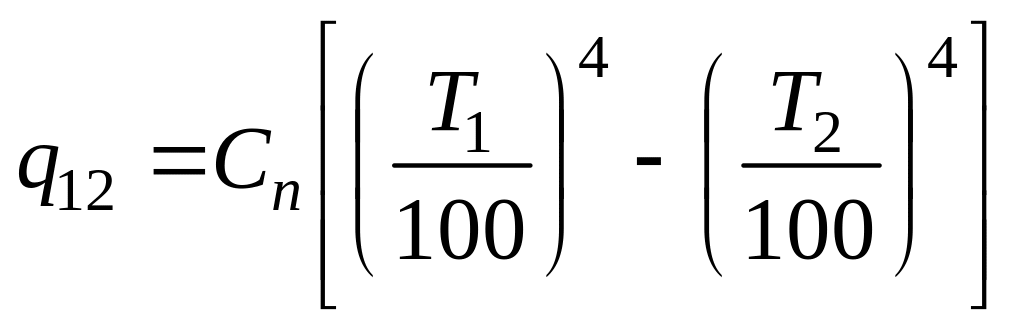
где

приведенный коэффициент лучеиспускания.
При наличии экрана количество тепла, передаваемое от первой поверхности к экрану

и от экрана к поверхности
 .
.
При установившемся
тепловом состоянии всей системы
![]()

Отсюда получаем уравнение

Выразим отсюда температуру экрана и получим
![]()
Это означает, что при наличии одного экрана количество передаваемого тепла уменьшается в 2 раза. При наличии n экранов - и (n+1) раз. Для большего эффекта используют экраны с малым значением коэффициента лучеиспускания.
