- •15. Плотность горных пород, как фактор, определяющий аномалии силы тяжести.
- •22. Решение прямой и обратной задачи маг-ки для вертикально намагниченной сферы.
- •2. Поле 2-х разнополярных источников постоянного тока.
- •3. Измерение уд эл сопротивления 4-х электродной установкой.
- •4. Понятие о кажущемся сопротивлении для неоднородной среды.
- •5. Удельное и кажущееся эл-е сопротивления.
- •6. Распределение плотности тока с глубиной. Идея вэз.
- •7. Вертикальное и дипольное эл-е зондирования.
- •8. Геоэлектрический разрез, эквивалентность кривых вэз.
- •10.Электрическое профилирование.
- •12. Продольная проводимость и поперечное сопротивление слоистого разреза.
- •13. Задачи, решаемые электроразведкой постоянным током.
- •15. Классификация эл-магнитных методов электроразведки.
- •16. Магнитотеллурические методы ( мтз и мтп).
- •17. Интерпретация данных мтз, мтп, тт.
- •18. Метод теллурических токов (мтт).
- •19. Идея частотного зондирования и решаемые им задачи.
- •21. Задачи, решаемые электроразведкой переменными эл-магнитными полями.
- •22. Геологические задачи, решаемые электроразведкой.
- •2. Волновое уравнение, продольные, поперечные волны, скорости их распространения.
- •3. Поле времен сейсмической волны, изохронны, лучи. Основное уравнение поля времен (ур-е Эйконала)
- •4. Принципы Гюйгенса-Френеля и Ферма.
- •5. Истинная и кажущая скорости распространения сейсм-х волн, связь м/у ними.
- •6. Отражение и прохождение сейсмических волн, монотипные и обменные волны.
- •9. Частотный диапазон сейсмических волн. Классификация методов по частотному диапазону.
- •10. Принцип устройства сейсм-й аппаратуры, сейсм-й канал, частотный и динамический диапазоны.
- •11. Отраженная волна от плоской наклонной границы на сейсмограмме опв.
- •12. Отраженная волна на сейсмограмме ост.
- •13. Понятие о многократных сейсмических волнах. Кратная волна на сейсмограммах ост и опв.
- •14. Понятие о дифрагированных волнах. Дифрагированная волна на сейсмограммах ост и опв.
- •15. Скорость ост, статические и кинематические поправки в трассы сейсмограмм ост. Временные сейсмические разрезы.
- •18. Для чего нужна сейсмическая миграция. Понятие о миграции Кирхгофа.
- •19. 3Д сейсморазведка, чем она лучше 2д?
- •20. Яркие пятна, как качественный способ сейсмической инверсии.
- •21. Пак, как способ ограниченной по частотному диапазону инверсии.
- •22. Понятие об упругой инверсии, avo анализ.
- •23. Уравнение годографа преломленной (головной) волны от наклонной границы, покрытой однородной средой.
- •24. Метод всп и решаемые им задачи.
- •25. Геологические задачи и области применения сейсморазведки.
1. Гравитационное поле Земли и его элементы, Г.П.З., поле силы тяжести; силовое поле, обусловленное притяжением (тяготением) Земли и центробежной силой, вызванной её суточным вращением. Зависит также (незначительно) от притяжения Луны, Солнца и др. небесных тел и масс земной атмосферы. Г.П.З. характеризуется силой тяжести (Fт; Р=Fпр+Fцб), потенциалом силы тяжести и различными производными от него. Потенциал имеет размерность см2.сек–2. За единицу измерения первых производных потенциала, в том числе силы тяжести, в гравиметрии принимается миллигал (мгл), равный 10–3 см.сек-2, а вторых производных — этвеш (Е), равный 10–9 сек–2, кот. характеризует изменение силы тяжести на 0,1 мГал на расстоянии 1 км. Часть потенциала силы тяжести, обусловленная только притяжением масс Земли, называется потенциалом земного притяжения, или геопотенциалом. Потенциал силы тяжести используется при изучении фигуры Земли, близкой к уровенной поверхности Г.П.З. (уровенной называется поверхность, во всех точках которой потенциал имеет одинаковое значение; сила тяжести направлена к ней по нормали). Одна из уровенных поверхностей, которая совпадает с невозмущённой средней поверхностью океанов, называется геоидом.
 F=G*m1m2/r2
F=G*m1m2/r2
G-гравитационная постоянная =66,7*10-12м3/(кг*с2); m1-масса Земли; m2-масса другого тела; в предположении, что r = 1 м. Сила тяжести и сила притяжения, различные понятия. На полюсе сила тяжести больше, чем на экваторе.
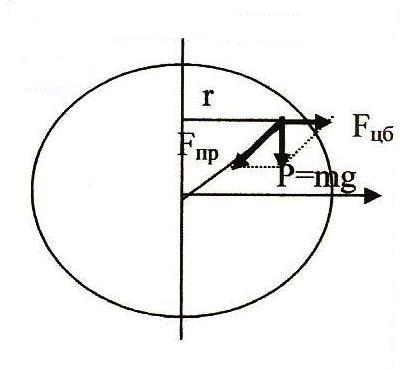
2. Сила тяжести и ее составляющие. Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести Fт=GMm/R2 ,где М - масса Земли; R - радиус Земли. Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле Fт=GMm/R2 модуль ускорения свободного падения g находят по формуле g=Fт/m=GM/R2. Из формулы g=Fт/m=GM/R2 следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы g=Fт/m=GM/R2 следует, что Fт = mg. В векторном виде Fт=mg . Поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы Fт=GMm/R2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе. Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела.
Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле
g=GM/(R+h) 2.
3. Сила притяжения и ее потенциал. Сила притяжения Fп , действующая между двумя массами, вычисляется согласно закону Ньютона. Для точечных масс m1 и m2, находящихся друг от друга на расстоянии r (r=1м), сила притяжения Fп=Gm1*m2/R2 и направлена по прямой, соединяющей эти массы. Константа G наз-ся гравитационной постоянной. G=66.7*10^(-12) м3/кг*с2. По физическому смыслу-это сила, кот-я действует м/у 2 единичными массами, кот-е наход-ся на расстоянии 1м.
Функция
V(x,y,z)
обладает свойством, что ее производные
по x,y,z
равны составляющим силы притяжения по
соот-щим осям координат, наз-ся потенциалом
притяжения.Частная производная от
потенциала притяжения по любому
произвольному направлению s
равна проекции силы притяжения на это
направление:
![]()
4.
Сила тяжести и ее потенциал. Силой
тяжести (![]() )
называют равнодействующую двух сил -
силы ньютоновского притяжения всей
массой Земли (
)
называют равнодействующую двух сил -
силы ньютоновского притяжения всей
массой Земли (![]() )
и центробежной силы, возникающей
вследствие суточного вращения Земли
(
)
и центробежной силы, возникающей
вследствие суточного вращения Земли
(![]() ).
Отнесенные к единице массы, эти силы
характеризуются ускорениями силы
тяжести g=F/m,
ньютоновского притяжения f=Fн/m
и центробежным P=P/m.
Ускорение силы тяжести равно геометрической
сумме ускорения притяжения и центробежного
ускорения.
).
Отнесенные к единице массы, эти силы
характеризуются ускорениями силы
тяжести g=F/m,
ньютоновского притяжения f=Fн/m
и центробежным P=P/m.
Ускорение силы тяжести равно геометрической
сумме ускорения притяжения и центробежного
ускорения.
Сила
притяжения какой-либо массы (![]() )
всей массой Земли (
)
всей массой Земли (![]() )
определяется законом всемирного
тяготения Ньютона: F=G*m1m2/r2
Где
r-
расстояние между центрами масс m
и M,
т.е. радиус Земли; g
- гравитационная постоянная, равная
G=6,67*10-11
м3/кг*с2.
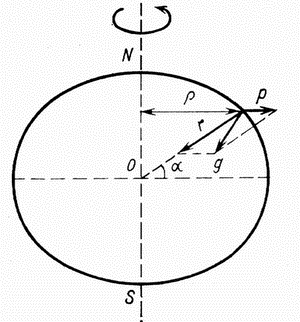
Величина P
изменяется от нуля на полюсе (R=0)
до максимума на экваторе. сила тяжести
почти целиком определяется силой
притяжения. Разная величина радиуса
Земли на полюсе и экваторе наряду с
изменением центробежной силы приводит
к увеличению g
на полюсе по сравнению с g
на экваторе.
)
определяется законом всемирного
тяготения Ньютона: F=G*m1m2/r2
Где
r-
расстояние между центрами масс m
и M,
т.е. радиус Земли; g
- гравитационная постоянная, равная
G=6,67*10-11
м3/кг*с2.
Величина P
изменяется от нуля на полюсе (R=0)
до максимума на экваторе. сила тяжести
почти целиком определяется силой
притяжения. Разная величина радиуса
Земли на полюсе и экваторе наряду с
изменением центробежной силы приводит
к увеличению g
на полюсе по сравнению с g
на экваторе.
.Потенциал силы тяж (W) -это интегральная функция, которая является мерой энергии затрачиваемой на перемещение единичной массы из каждой точки поля в бесконечность. g=-dW/dr, т.е. сила тяжести есть производная потенциала силы тяжести по направлению к центру Земли. Поэтому гравитационное поле можно представить в виде набора бесконечного числа поверхностей, на которых потенциал остается постоянным, а ускорение силы тяжести направлено перпендикулярно этой поверхности. Такие поверхности называют эквипотенциальными или уровенными. У Земли есть одна уровенная поверхность, которая совпадает с невозмущенной волнениями поверхностью океанов. Она называется геоидом. геоид - это условная уровенная поверхность, которая совпадает со средним уровнем океанов и открытых морей, проходит под сушей и по определению везде горизонтальна, а ускорение силы тяжести к ней перпендикулярно.
5. Вторые производные потенциала силы тяжести, их физический смысл и геологоразведочное значение. Производные потенциала силы тяжести по трем координатным осям gx=∂W/∂x; gy=∂W/∂y; gz=∂W/∂z; однозначно определяют его полный вектор. В частности, если ось z направить к центру Земли, то ∂W/∂x=∂W/∂y=0; а g=∂W/∂x. В гравиметрии кроме первых производных изучаются вторые производные потенциала или их разности: ∂2W/∂x∂y; ∂2W/∂x∂z; ∂2W/∂y∂z; ∂2W/∂x2; ∂2W/∂y2; ∂2W/∂z2; ∂2W/∂x2 – ∂2W/∂y2. Те производные, кот имеют dz, наз. Градиентами сил тяжести и применяются для разведочных целей в гравиразведке; Остальные прим-ся для изучения фигуры (формы) Земли. Фигуру земли можно изучать только по гравитационному полю. Физический смысл этих выражений легко получить, если иметь в виду, что g=∂W/∂z. Так вторая производная ∂2W/∂x∂z=∂g/∂x указывает на скорость изменения силы тяжести по оси х, т.е. является гори-зонтальным градиентом силы тяжести. Полный горизонтальный градиент силы тяжести это квадратный корень из Wг=W2xz+W2yz Аналогичный смысл имеют вторые производные ∂2W/∂x∂z и ∂2W/∂z2
Практической единицей измерения градиента силы тяжести принимается 1 этвеш(Е), что соответствует изменению силы тяжести в 0,1 мГал на 1 км. Вторые производные потенциала силы тяжести применяются при решении геологоразведочных и геодезических задач. Аномальная часть вторых произ-водных потенциала позволяет судить о плотностных неоднородностях в верхних частях земной коры.
6. Нормальные значения силы тяжести. Нормальным значением силы тяжести (γ0) называется сила тяжести, обусловленная суточным вращением и притяжением Земли, в предположении, что она состоит из однородных по плотности концентрических слоев. Принимая Землю за сфероид, Клеро получил следующую приближенную формулу для ее расчета: γ0=gэ(1+βsin2φ), где gэ- сила тяжести на экваторе; φ- географическая широта пункта наблюдения; β- коэффициент, зависящий от угловой скорости вращения и сжатия сфероида. Однако Земля - геоид, и нормальные значения силы тяжести для его поверхности рассчитываются по формуле: γ0=gэ(1+βsin2φ- β1sin22φ+ β2cos2φcos2λ); где λ- географическая долгота точки наблюдения. Коэффициенты β, β1 и β2 зависят от формы Земли, ее угловой скорости вращения, распределения масс. Измерив g_н в какой-то точке и вычтя γ0, получим аномалию силы тяжести. Таким образом, геоид является поверхностью относимости, по отношению к которой рассчитываются аномалии.
7. Редукции и аномалии силы тяжести. В наблюденные значения силы тяжести вводятся поправки (редукции). Введение поправок необходимо потому, что нормальные значения относятся к поверхности геоида, которая совпадает с уровнем океана, а измеренные значения относятся к действительной (реальной) земной поверхности. Для того, чтобы все наблюдения силы тяжести были сопоставимы, их приводят к одной поверхности - уровню геоида, т.е. как бы опускают точку наблюдения на этот уровень. Это осуществляется путем введения поправок за высоту, за притяжение промежуточного слоя и окружающий рельеф. Поправки называются редукциями. Основными из них являются: поправка за высоту, за притяжение промежуточного слоя, за рельеф. Для приведения измеренного значения gн к уровню океана вводят поправку за высоту(∆g). Эту поправку называют поправкой за "свободный воздух" или поправкой Фая. Эта поправка должна прибавляться к измеренной силе тяжести, если точка наблюдений находится выше уровня геоида, и вычитаться, если ниже. При введении поправки за притяжение промежуточного слоя (∆g2) вычисляется притяжение масс слоем между уровнем океана и данной точкой. Для учета бокового притяжения рельефа местности, окружающего пункт наблюдения, при съемке в горных районах вводятся топографические поправки (∆g3). В геодезической гравиметрии под аномалией силы тяжести понимают разность между наблюденным значением (gн) и нормальным (γ0) с учетом поправки Фая, она рассчитывается по формуле ∆gф~gн-γ0+g1 и называется аномалией Фая. Основной аномалией в гравиразведке является аномалия Буге: ∆gБ=gн-γ0+ ∆g1+ ∆g2+∆g3= gн-gтеор; в которую вводятся все поправки.
8.
Аномалии силы тяжести Бугэ.
Поправка Бугэ=попр за высоту (Фая)+попр
за промежуточный слой +попр за рельеф.
Основной аномалией в гравиразведке
является аномалия Буге: ∆gБ=gн-γ0+
∆g1+
∆g2+∆g3=
gн-gтеор;
в которую вводятся все поправки. Под
gтеор
понимается суммарная поправка в
наблюденные значения, которая может
быть определена до проведения работ,
поскольку в ней имеются лишь топографические
координаты точек наблюдения (φ,Н). Ее
рассчитывают с помощью ЭВМ.
При вычислении аномалий Буге следует
различать два случая: 1) точка наблюдения
расположена на суше; 2) точка наблюдения
расположена на море. В первом случае
для точек 1, 2, 5, 6, расположенных на суше,
аномалия Буге вычисляется по формуле:
![]() Для
точек 3 и 4, расположенных на море, поправка
за влияние промежуточного слоя вычисляется
по формуле:
Для
точек 3 и 4, расположенных на море, поправка
за влияние промежуточного слоя вычисляется
по формуле:
![]() Аномалия
Буге в этом случае вычисляется по
формулам
с учетом
Аномалия
Буге в этом случае вычисляется по
формулам
с учетом ![]() ,
вычисленной по формуле
,
вычисленной по формуле
9. Геологические факторы, формирующие аномалии Буге. Аномалию Буге вычисляют как разность между наблюденным и нормальным значениями силы тяжести с введением суммарной поправки за высоту и промежуточный слой бgБ=бgh+бgo. После вычитания из наблюденного поля нормального значения силы тяжести и поправки Буге оставшаяся его часть-аномалия силы тяжести- характеризует влияние залегающих внутри Земли плотностных неоднородностей. Изучив рас-пределение аномалий на поверхности Земли, можно получить информацию о ее внутреннем строении. Большую роль при вычислении аномалии Буге играет выбор плотности промежуточного слоя: если плотность принять слишком малой, то возможна прямая корреляционная зависимость значений аномалий от рельефа физической поверхности; если же плотность слоя сильно завышена, то будет наблюдаться отрицательная корреляционная зависимость. При вычислении аномалий силы тяжести за одно из значений плотности промежуточного слоя берут среднее значение плотности земной коры-2,67 г/см3. Для геологической интерпретации рекомендуется вычислять аномалии Буге с истинной (реальной) плотностью промежуточного слоя, полученной в условиях естественного залегания горных пород.
10. Способы трансформации гравитационного поля и их сущность. Наблюденное гравитационное поле представляет сумму аномалий, созданных различными возмущающими массами: ∆ga=∆1ga+∆2ga+…+∆kga+…+∆nga=∑∆kga, где ∆kga – аномалия, обусловленная одной из возмущающих масс. Для обнаружения в суммарном гравитационном поле аномалии от интересующей геологической структуры нужно, чтобы ее интенсивность преобладала над интенсивностью аномалий от всех других возмущающих масс. Операции по разделению гравитационных аномалий можно разделить на 3 класса: 1. аналитическое продолжение наблюденного поля аномалий силы тяжести на новые уровни – на плоскость, расположенную выше плоскости наблюдений (аналитическое продолжение в верхнее полупространство), или на плоскость, расположенную ниже плоскости наблюдений ( аналитическое продолжение в нижнее полупространство). 2. Усреднение аномального поля. 3. Вычисление высших производных потенциала силы тяжести (вертикальных и горизонтальных). Применение высших производных потенциала силы притяжения позволяет в ряде случаев выявить локальные аномалии, обусловленные малоамплитудными структурами в осадочной толще, а при благоприятных условиях – и крупные нефтегазовые залежи.
11. Качественная и количественная интерпретация данных гравиразведки. Качественная интерпретация. Первым этапом интерпретации результатов гравиразведки является качественная интерпретация. При качественной интерпретации дается визуальное описание характера аномалий силы тяжести по картам и профилям, т.е. отклонений от средних (фоновых) значений ∆gБ. Устанавливается связь гравитационных аномалий с геологическим строением, выделяются региональные аномалии, связанные со строением земной коры, и локальные аномалии, часто представляющие большой разведочный интерес. Выделение региональных аномалий от локальных называется снятием регионального фона. Оно производится, как правило, графическим путем.
Количественная
интерпретация. 1.
Общие
положения.
Определение глубины, формы, размеров и
точного местоположения геологических
тел, создающих наблюденные аномалии,
составляет основную цель количественной
(расчетной) интерпретации, основанной
на методах решения обратной задачи
гравиразведки. Решение обратной задачи
неоднозначно, так как одинаковые аномалии
силы тяжести могут быть созданы
геологическими объектами разной формы,
размеров и плотности. Методы решения
обратной задачи гравиразведки принято
подразделять на прямые, в которых
элементы залегания гравитирующих масс
определяются непосредственно по картам
и графикам
![]() (или
вторых производных потенциала), и
косвенные, когда наблюденные аномалии
сравниваются с набором теоретически
рассчитанных аномалий над определенными
объектами, и методом последовательных
приближений добиваются наилучшего
совпадения полей.
(или
вторых производных потенциала), и
косвенные, когда наблюденные аномалии
сравниваются с набором теоретически
рассчитанных аномалий над определенными
объектами, и методом последовательных
приближений добиваются наилучшего
совпадения полей.
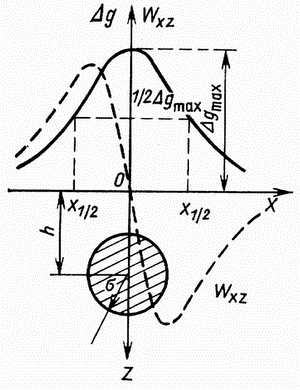
12. Решение прямой задачи гравиразведки на примере однородного шара. Пусть однородный шар радиуса a и плотности σ расположен на глубине h в среде с плотностью σ0 (для простоты центр находится на оси z, а наблюдения проводятся по оси x в точке P) (рис. 1.).
|
Рис.1. Гравитационное поле шара |
Формула для вычисления g может быть получена из ∆g=ƒcosα=G*dm/r2*z/-z/r; ∆g=-∂W/∂z=Gdm(z/-z)/r3; ∆g=Gdv/r3*(z/-z); ∆g=G(σ-σ0)*dv/r3*(z/-z); путем замены элемента dm массой шара в силу того, что притяжение однородным шаром происходит так, как если бы вся масса была сосредоточена в центре шара. Учтя, что x'=y'=0,z'=h,y=z=0, получим для шара ∆g=GMh/r3=G(σ-σ0)Vh/r3=G(σ-σ0)Vh/(x2+h2)3/2 График ∆g будет иметь максимум над шаром (x=0) и асимптотически стремиться к нулю при удалении от шара. В плане изолинии будут иметь ∆g вид концентрических окружностей. Вторая производная (градиент аномалии по профилю наблюдений) равна: Wxz=∂(∆g)/∂x=GMh∂(1/r3)/∂x=-3GMhx/r3 Вид кривой Wxz может быть легко получен путем графического построения из кривой ∆g. График Wxz имеет перед шаром максимум, за шаром - минимум, над центром шара - ноль.
13. Решение обратной задачи гравиразведки на примере однородного шара. Пусть однородный шар радиуса a и плотности σ расположен на глубине h в среде с плотностью σ0 (для простоты центр находится на оси z, а наблюдения проводятся по оси x в точке P) (рис. 1.).
|
Рис.1. Гравитационное поле шара |
Формула для вычисления g может быть получена из ∆g=ƒcosα=G*dm/r2*z/-z/r; ∆g=-∂W/∂z=Gdm(z/-z)/r3; ∆g=Gdv/r3*(z/-z); ∆g=G(σ-σ0)*dv/r3*(z/-z); путем замены элемента dm массой шара в силу того, что притяжение однородным шаром происходит так, как если бы вся масса была сосредоточена в центре шара. Учтя, что x'=y'=0,z'=h,y=z=0, получим для шара ∆g=GMh/r3=G(σ-σ0)Vh/r3=G(σ-σ0)Vh/(x2+h2)3/2 График ∆g будет иметь максимум над шаром (x=0) и асимптотически стремиться к нулю при удалении от шара. В плане изолинии ∆g будут иметь вид концентрических окружностей. Из ∆g=GMh/r3=G(σ-σ0)Vh/r3=G(σ-σ0)Vh/(x2+h2)3/2 максимум ∆g над центром шара (x=0) равен ∆gmax=GM/h2. Для точки, удаленной от максимума на расстояние x1/2, имеющей ∆g1/2=1/2∆gmax, можно записать следующее уравнение: ∆g1/2=GM/2h2=GMh/(x21/2+h2)3/2 или 2h3=(x21/2+h2)3/2 Решив последнее уравнение, получим формулу для определения глубины залегания центра шара h=1,3x1/2. Зная h, легко найти избыточную массу (M): M=∆gmaxh2/G.. Так как M=V(σ-σ0)=4/3πa3(σ-σ0) то, зная избыточную плотность (σ-σ0), можно рассчитать объем (V) и радиус шара (a). Так, радиус равен:
|
14. Решение прямой задачи гравиразведки для контактной поверхности. Контактной наз пов-ть раздела двух сред бесконечного простирания с различной плотностью, причем нижняя среда имеет бесконечную мощность.
R
R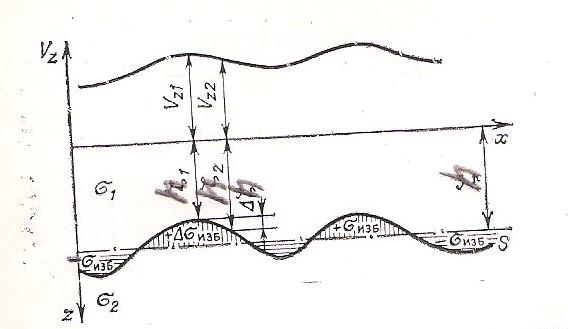
Рис. 1. Гравитационное поле контактной поверхности.
Пусть (рис.1.) граница RR является следом сечения вертикальной плоскостью пов-ти двух толщ: верхней, с конечной мощностью и плотностью б1 и нижней, бесконечной мощности и плотностью б2. Проведем горизонтальную линию на глубине h. Притягивающие массы, залегающие выше горизонтальной линии, имеют положительную избыточную плотность б, ниже-отрицательную. Гравитационное притяжение контактной поверхности можно представить в виде суммы притяжений бесконечного плоско-параллельного слоя мощностью h и плотностью бизб и масс, заключенных между горизонтальной линией и рельефом границы: Vz=2π G(σ2-σ1)*h+∑δVz. Приближенная формула, для относительно спокойного рельефа границ: ∆Vz=Vz2-Vz1=2πGσизб(h2-h1), где ∆Vz-приращение силы притяжения в двух точках х1 и х2; h1-глубина залегания контактной поверхности в точке х1; h2- глубина залегания той же поверхности в точке х2. Последнюю формулу широко применяют при оценке по данным гравиразведки характера залегания границ раздела плотности в случае разрезов, близких к горизонтально-слоистым.
15. Плотность горных пород, как фактор, определяющий аномалии силы тяжести.
Гравитационные аномалии возникают только в том случае, если ГП, слагающие земную кору, различаются по плотности и границы между ними не горизонтальны. Дифференциация пород разреза по значениям плотности определяет возможность применения и эффективность гравиразведки: чем различнее по плотности породы, слагающие структуру, и вмещающие, тем больше гравитационная аномалия, создаваемая этой структурой. Разность плотностей вмещающих пород и пород структуры, создающей аномалию, называется избыточной плотностью . В гравиразведке рассматривается объемная плотность ГП, кот определяется как отношение массы m ГП к ее объему V: σ=m/V. Средняя плотность земной коры составляет 2,67 г/см3. Земли – 5,52 г/см3. Плотность ГП увеличивается в след последовательности: осадочные - кислые изверженные - основные изверженные - метаморфические.
16.Принцип устройства гравиметра. Гравиметры-это устройства, которые используются при статических методах измерения силы тяжести:действие силы тяж компенсируется упругими силами пружин, газов или жидкости и т.п.Гр-ры предназначены для измерения приращения силы тяж м/у 2 пунктами, с точностью до 0,01 мгал. В гравиразведке в основном применяют гр-ры с пружиными чувствительными системами. Принцип устройства кварцевого астазированного гравиметра «ГАК». На тонкой нити(она ось вращения) укреплен маятник. Он удерживается в исходном положении силой натяжения главной пружины, нижний конец которой через рычаг прикреплен к маятнику, и силой закручивания нити подвеса маятника. При изменении силы тяж маятник прибора отклоняется от положения, растягивая главную пружину и закручивая нить подвеса до тех пор, пока момент силы тяжести не будет уравновешен моментом главной пружины и моментом закручивания нити подвеса. При измерении силы тяж маятник возвращают в исходное положение, вводя в систему дополнительный момент, компенсирующий изменение силы силы тяж в данном пункте относительно исходного пункта.
17.
Силы магнитного взаимодействия, потенциал
и напряженность магнитного поля.
Потенциал магнитного поля Т=∂U/∂r,
где Т – напряженность магнитного поля;
∂U – магнитный потенциал; ∂r
– расстояние. Составляющие магнитного
поля, выраженные через потенциал:
X=∂U/∂x;
Y=∂U/∂y;
Z=∂U/∂z.
Значение магнитного потенциала точечной
массы: U=m/(μr).
Потенциал, создаваемый элементарным
диполем dU:
dU=m1/μr1-m2/μr2=m(r2-r1)/μr1r2=dM/μr2*cosθ;
т.к. r1=r2;
2mdl=dM;
r2-r1=2dlcosθ,
с учетом этих выражений в итоге получим:
dU=m1/μr1-m2/μr2
.
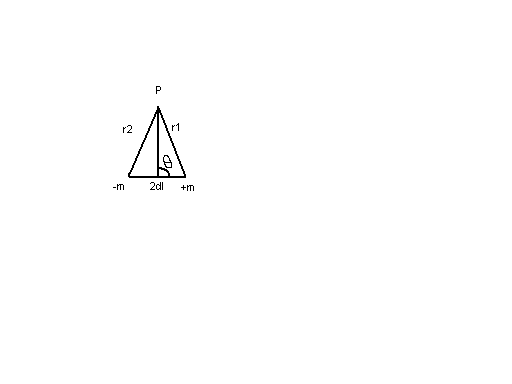
Напряженность магнитного поля (А/м): Сила взаимодействия между изолированными точечными магнитными массами, определяемая законом Кулона: F=m1m2/μr2, где μ – магнитная проницаемость; m1 и m2 – точечные магнитные массы; r – расстояние между ними. Сила, действующая на единичную магнитную массу, наз напряженностью магнитного поля Т. Приняв в F=m1m2/μr2 m1=1, получим: Т=m/μr2/.
18. Геомагнитное поле и элементы земного магнетизма. геомагнитное поле Земли можно разделить на следующие 4 основные части. 1. Основное магнитное поле Земли, испытывающее медленные изменения во времени (вековые вариации) с периодами от 10 до 10 000 лет. 2. Мировые аномалии – отклонения от эквивалентного диполя до 20% напряженности отдельных областей с характерными размерами до10 000 км. Эти аномальные поля испытывают вековые вариации, приводящие к изменениям со временем в течение многих лет и столетий. 3. Магнитные поля локальных областей внешних оболочек с протяженностью от нескольких до сотен км. Они обусловлены намагниченностью горных пород в верхнем слое Земли, слагающих земную кору и расположенных близко к поверхности. 4. Переменное магнитное поле Земли (внешнее) определяется источниками в виде токовых систем, находящимися за пределами земной поверхности и в ее атмосфере. Тн=Тg+Tm+Ta+Tвн+Те; Тg – дипольное поле земли; Tm – поле мировых магнитных аномалий; Ta – поле локальных и региональных аномалий; Tвн – поле, обусловленное внешними причинами (причины, связанные с Солнцем); Те – вариации магнитного поля во времени; Тн – наблюденное поле. Дипольное поле – это внутренне магнитное поле земли. Поле мировых магнитных аномалий: Тg+ Tm+ Те – нормальное магнитное поле. Составляющие магнитного поля:
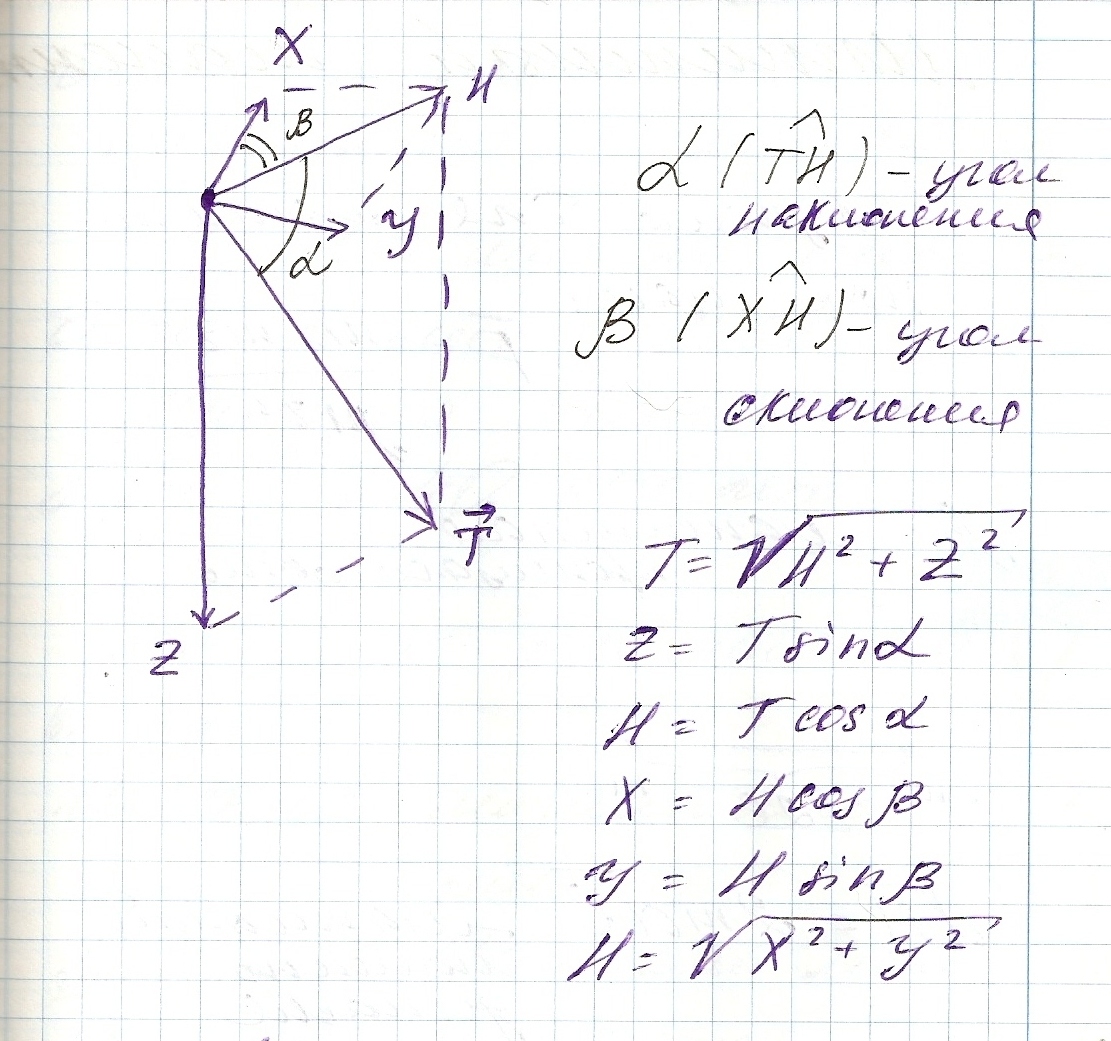
Угол между осью Х и составляющей Н называется склонением и обозначается β (^ТН). Угол между вектором Т и горизонтальной плоскостью называется наклонением и обозначается α (^ХН).
19. Структура магнитного поля Земли. Земное магнитное поле находится под воздействием потока намагниченной солнечной плазмы. В результате взаимодействия с полем Земли образуется внешняя граница околоземного магнитного поля, называемая магнитопаузой. Она ограничивает земную магнитосферу. Из-за воздействия солнечных корпускулярных потоков размеры и форма магнитосферы постоянно меняются, и возникает переменное магнитное поле, определяемое внешними источниками. Его переменность обязана своим происхождением токовым системам, развивающимся на различных высотах от нижних слоев ионосферы до магнитопаузы. Изменения магнитного поля Земли во времени, вызванные различными причинами, называются геомагнитными вариациями, которые различаются как по своей длительности, так и по локализации на Земле и в ее атмосфере. Магнитосфера – область околоземного космического пространства, контролируемая магнитным полем Земли. Магнитосфера формируется в результате взаимодействия солнечного ветра с плазмой верхних слоев атмосферы и магнитным полем Земли. Магнитопауза – внешняя граница магнитосферы Земли (или планеты), на которой динамическое давление солнечного ветра уравновешивается давлением собственного магнитного поля.
20. Нормальное геомагнитное поле. Магнитные аномалии. В первом приближении магнитное поле Земли может быть уподоблено полю однородно намагниченного шара, или полю диполя (Т0), расположенного в области центра Земли. Ось такого диполя по отношению к оси вращения Земли составляет 11,50. Места выхода продолжений оси этого диполя на земную поверхность называют геомагнитными полюсами. Геомагнитное поле Земли заметно отличается от поля диполя, образуя по крайней мере 4 мощные геомагнитные аномалии. Их называют материковыми, или континентальными (Тм), а происхождение связывают с наличием дополнительных магнитных диполей на верхней) и нижней границах "жидкого" ядра. Нормальным (или главным) геомагнитным полем (Тн) принято считать поле однородно намагниченного шара (То) и дополнительных диполей в ядре, обуславливающих материковые аномалии (Тм), т.е. Тн=Т0+Тм. Магнитные аномалии: Отклонения наблюденных значений магнитных векторов (Т) от нормального поля будут составлять аномалии региональные (Тр) или локальные (Тл) в зависимости от площади, на которых они получены: Та=Т-Тн=Тр+Тл. Региональные и локальные аномалии бывают положительными и отрицательными. Таким образом, полное постоянное магнитное поле Земли(Т) складывается из нормального и аномального полей:Т=Т0+Тм+Тр+Тл=Тн+Та.
21. Магнитный потенциал и его связь с гравитационным потенциалом. Гравитационный потенциал притяжения: V=Gσ∫dΩ/r. Магнитный потенциал (ф-ла Пуассона): U=1/Gσ*IdV/dr. При использовании данной формулы, следует заметить, что есть интенсивность намагничивания I, и если I=0, то и U=0, следовательно данная формула имеет смысл, если I≠0. Связь магнитного потенциала с гравитационным выражается с помощью формулы пуассона, смысл которой заключен в том, что магнитный потенциал однородно намагниченного тела равен производной гравитационного потенциала этого же тела, взятой по направлению намагничивания. Формула позволяет при вычислении магнитных полей опираться на решения, кот-е были получены для прямой задачи гравиразведки.