14 Коэффициент корреляции: формула, интерпретация, условия применимости

Коэффициент корреляции является одним из самых востребованых методов математической статистики в психологических и педагогических исследованиях. Формально простой, этот метод позволяет получить массу информации и сделать такое же количество ошибок. В этой статье мы рассмотрим сущность коэффициента корреляции, его свойства и виды.

Коэффициент корреляции — это мера взаимосвязи измеренных явлений.

Коэффициент корреляции (обозначается «r») рассчитывается по специальной формуле и изменяется от -1 до +1. Показатели близкие к +1 говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной. Показатели близкие к -1 свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются.

Он рассчитывается следующим образом:

Есть массив из n точек {x_1,i, _x2,i}

Рассчитываются средние значения для каждого параметра: 

И коэффициент корреляции: 

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x₁ и x₂: rравен 1 (или -1), если связь линейна.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:

1. Коэффициент корреляции значимо отличается от нуля (т.Е. Есть взаимосвязь между величинами):

Тестовая статистика вычисляется по формуле:

и сравнивается с табличным значением коэффициента Стьюдента t(p = 0.95, f =  ) = 1.96

Если тестовая статистика больше табличного значения, то коэффициент значимо отличается от нуля. По формуле видно, что чем больше измерений n, тем лучше (больше тестовая статистика, вероятнее, что коэффициент значимо отличается от нуля)

2. Отличие между двумя коэффициентами корреляции значимо:

Тестовая статистика:

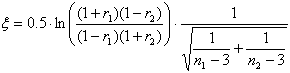
Также сравнивается с табличным значением t(p, )

Методами корреляционного анализа решаются следующие задачи:

1) Взаимосвязь. Есть ли взаимосвязь между параметрами?

2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.

3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.

15 Коэффициенты связи двух номинальных признаков: основанные на критерии “Хи-квадрат”, на моделях прогноза. Коэффициенты связи для 4-х-клеточных таблиц

Критерий хи-квадрат имеет несколько разновидностей:

1. Likelihood Ratio (Отношение правдоподобия). Данный критерий является более устойчивым к объему выборки, чем хи-квадрат.

2. Linear-by-Linear Association (Линейно-линейная связь). Данная разновидность критерия хи-квадрат подходит только для количественных переменных.

Меры связи, основанные на критерии «Хи-квадрат».

Меры связи – коэффициент позволяющий оценить силу направление связей для номинальных признаков.

Коэффициент сопряженности признаков (Пирсона)

Его величина всегда находится в пределах от 0 до 1 и вычисляется (как и значения критериев Фишера (<р) и Крамера (V)) с использованием значения критерия хи-квадрат:

 

Здесь N — общая сумма частот в таблице сопряженности. Так как N всегда больше нуля, коэффициент сопряженности признаков никогда не достигает единицы. Максимальное значение зависит от количества строк и столбцов таблицы сопряженности и в таблице размером 3*2 составляет (как в данном примере) 0,762. По этой причине коэффициенты сопряженности признаков для двух таблиц с разным количеством полей несопоставимы. Contingency Coefficient (Коэффициент Контингенции). Эта мера применима для любой таблицы, так как ее значения всегда лежат между 0 и 1, тем не менее, она имеет по сравнению с коэффициентом «фи» другой недостаток. Коэффициент контингенции никогда не может достичь верхней границы, равной единице. Максимально возможное значение такой меры зависит от числа строк и столбцов таблицы. Например, для таблицы 4´4 максимальное значение коэффициента контингенции равно только 0,87.

Критерий Фишера (<р)

Этот коэффициент можно использовать только для таблиц 2*2, так как в других случаях он может превысить значение 1:

Критерий Крамера (V)

Этот критерий представляет собой модификацию критерия Фишера и для любых таблиц сопряженности он дает значение в пределах от 0 до 1, включая 1:

 

Здесь k — наименьшее из количеств строк и столбцов.

Три названных критерия основаны на использовании критерия хи-квадрат. Они различными способами нормируют его значение по отношению к размеру выборки. Так, если формуле для V Крамера положить k = 2, то значения (р и V Крамера совпадут. Определение значимости основано на значении критерия хи-квадрат.

При оценке полученных значений мер связанности, находящихся в нашем примере в промежутке между 0,4 и 0,5, следует учесть, что значение 1 достигается очень редко или вообще никогда. Другие меры связанности (Я, т Гудмена-Крускала и коэффициент неопределенности) определяются на основе так называемой концепции пропорционального сокращения ошибки. При определении этих критериев одна переменная рассматривается как зависимая; по этой причине данные критерии называются "направленными мерами".

Коэффициент Пирсона c2 

Коэффициент p принимает значение, равное нулю, как и все остальные коэффициенты, основанные на c2-статистике, тогда и только тогда, когда отмечается полная независимость признаков. Однако использование данного коэффициента является абсолютно корректным по всем позициям только для таблиц 2´2. В этом случае коэффициент Пирсона p равен стандартному коэффициенту корреляции. Для таблиц размером больше двух он может принимать значения больше единицы, так как критерий c2 принимает значение, превышающее значение объема выборки

Особенности применения, ограничения, достоинства и недостатки.

Все коэффициенты изменяются от 0 до 1 и равны нулю в случае полной независимости признаков (в описанном выше смысле). Как и критерий “хи-квадрат”, эти показатели являются симметричными относительно наших признаков: с их помощью нельзя выделить зависимую и независимую переменную, на основе их анализа нельзя говорить о том, какая переменная на какую "влияет". На них накладываются те же ограничения, что и на c2. значение мер имеет ту же значимость, что и значение c2.. Величина Пирсона (СС) зависит от размерности таблицы. Наиболее устойчивой к размерам таблицы является Критерий Крамера (V)

Меры связи, основанные на моделях прогноза:

Коэффициенты , основанные на модальном прогнозе

Формализуем понятие прогноза следующим образом. Выбирая произвольный объект и зная распределение рассматриваемого признака (условное или безусловное), считаем, что для выбранного объекта этот признак принимает то значение, которое имеет максимальную вероятность, встречается с максимальной частотой (т.е. модальное значение). Такой прогноз называется мод а льным. Чтобы стал ясен содержательный смысл рассматриваемого прогноза, приведем формулы соответствующих коэффициентов. Но сначала отметим, что таких коэффициентов три: два отражают возможные направленные связи, а третий является их усреднением. Эти коэффициенты обычно обозначаются буквами l с индексами: l r – отражающий “влияние” строкового признака на столбцовый; l с – отражающий "влияние" столбцового признака на строковый, l – усредненный коэффициент.

Общее представление о пропорциональном прогнозе

Представленное понимание прогноза не является единственно возможным. Более того, его нельзя признать наилучшим. Прогноз здесь очень груб, приблизителен. Используя достижения теории вероятностей, к определению понятия прогноза можно подойти более тонко. Опишем еще один подход. На нем тоже базируется целый ряд известных коэффициентов связи (например, коэффициент Валлиса [Интерпретация и анализ ..., 1987; Статистические методы ..., 1979]). Принцип их “действия” по существу является тем же, что и принцип l -коэффициентов. Отличие состоит только в понимании процедуры прогноза. Мы не будем эти коэффициенты описывать, поскольку такое описание требует использования довольно сложных формул, но ничего не дает принципиально нового для понимания отражаемой с помощью этих коэффициентов связи.

Итак, что же такое пропорциональный прогноз? Опишем его суть с помощью примера.

Предположим, что мы имеем дело с частотной табл. 1 3. Рассмотрим безусловное распределение Y. Обратимся к схематичному изображению ситуации в терминах столь часто фигурирующих в литературе по теории вероятностей урн и заполняющих их шаров. Возьмем 150 шаров, на 45 из них напишем цифру 1, на 40 - цифру 2, на 65 - цифру 3 и погрузим все шары в урну, перемешав их. Правило прогноза выглядит очень просто: берем случайного респондента, опускаем руку в урну и вытаскиваем тот шар, который случайно же нам попался. То, что на нем написано, и будет прогнозным значением признака Y для выбранного респондента . Аналогичным образом поступаем и для каждого условного распределения. Конечно, реализовать такой подход можно и без шаров с урнами, но суть должна сохраниться: то, что чаще встречается в исходной совокупности, должно чаще попадаться в наши руки при вытаскивании шаров. К примеру, в соответствии с первым условным распределением (Х=1, первая строка частотной таблицы), у нас отсутствуют респонденты, для которых Y = 1. Не будут попадаться нам и шары с единицей, поскольку количество таких шаров равно 0. В соответствии с третьим распределением (Х=3) значения 2 и 3 признака Y встречаются одинаково часто и в 8 раз реже значения 1. И вероятность встречаемости шаров с цифрами 2 и 3 будет одинаковой и в 8 раз меньше вероятности встречаемости шара с 1.

Описанный прогноз называется пропорциональным. Хотя соответствующее правило на первый взгляд, довольно сложно, оно позволяет предсказывать значение зависимого признака с большей надежностью, чем правило модального прогноза. Это часто используется в самых разных прогнозных алгоритмах.

Четырехклеточные таблицы.

Четырехклеточные таблицы – это частотные таблицы, построенные для двух дихотомических признаков. Ведь они представляют собой частный случай всех возможных таблиц сопряженности