
- •8.Предел числовой последовательности и общие свойства предела.
- •9.Предельный переход и арифметические операции.
- •11.Критерий Коши существования предела числовой последовательности.
- •12.Существование предела монотонной ограниченной последовательности.
- •13.Подпоследовательность.Теорема Больцано-Вейерштрасса о выделении сходящейся подпоследовательности.
- •14.Предел функции. Эквивалентность определений по Коши и по Гейне.
- •15. Общие свойства предела функции и арифметические операции.
- •16.Предел функции и неравенства.
- •17.Односторонние пределы.
14.Предел функции. Эквивалентность определений по Коши и по Гейне.
Определение.(по
Коши)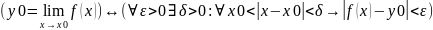
Определение.(по
Гейне)
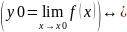
Доказательство эквивалентности:
Пусть
y0 есть предел функции f(x) при x → x0 по
Гейне, т.е. ∀
{
}
:
→
x0 при
n →
∞
следует,
что
f(
)
→
y0 при
n →
∞.
Пусть
y0 не
есть
предел
функции
f(x) при
x →
x0 по
Коши,
т.е.
∃ε
> 0 ∀δ
> 0 ∃x
∈
˙
Vδ(x0)
⇒
|f(x)−y0|
>= ε.
Возьмем
δn
= 1/n, n = 1,2,... и найдем
∈
˙
Vδn(x0),
где
при
этом
будем
иметь
|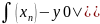 >= ε.
Значит
имеем
{
}
такую,
что
→
x0 при
n →
∞
и
кроме
того
|
>= ε.
Значит
имеем
{
}
такую,
что
→
x0 при
n →
∞
и
кроме
того
|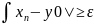 ,
что
противоречит
определению
по
Гейне.
,
что
противоречит
определению
по
Гейне.
15. Общие свойства предела функции и арифметические операции.
Свойства:
а) Если y0 предел функции f(x) при x → x0, то f(x) финально ограничена при x → x0;
б) Если f(x) финально постоянна при x → x0 то она имеет предел в точке x0;
в) Если f(x) в точке x0 имеет предел, то этот предел единственный. а) Если функции f : X → R и g : X → R таковы, что lim x→x0 f(x) = y0, lim x→x0
g(x) = y1 и y0 < y1 то найдется проколотая окрестность V˙δ(x0) точки x0, в любой точке которой выполнено неравенство f(x) < g(x).
б) Если между функциями f : X → R, g : X → R и h : X → R на множестве X имеет место соотношение
f(x) g(x) h(x) и если lim x→x0 f(x) = lim x→x0 h(x) = y0, то существует также предел функции g(x) при x → x0, причем limx→x0 g(x) = y0. Следствие. Пусть limx→x0 f(x) = y0, limx→x0 g(x) = y1. Если в некоторой проколотой окрестности V˙δ(x0) точки x0:
а)
f(x)
 g(x), то y0
y1;
g(x), то y0
y1;
б) f(x) g(x), то y0 y1;
в) f(x) y1, то y0 y1;
г) f(x) y1, то y0 y1.
16.Предел функции и неравенства.
Число
y0
называется пределом функции y = f(x) в
точке x0
(или, при x → x0),
если для любого ε > 0 можно указать
такое число δ = δ(ε) > 0, что при всех x,
удовлетворяющих условию 0 < |x − x0|
< δ, выполняется неравенство |f(x) − y0|
< ε, или: y0=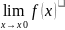 ⇔
∀ε
> 0 ∃δ
> 0 : ∀x
0 < |x − x0|
< δ ⇒
|f(x) − y0| < ε .
⇔
∀ε
> 0 ∃δ
> 0 : ∀x
0 < |x − x0|
< δ ⇒
|f(x) − y0| < ε .
а) Если y0 предел функции f(x) при
x → x0, то f(x) финально ограничена при x → x0; б) Если f(x) финально постоянна при x → x0 то она имеет предел в точке x0; в) Если f(x) в точке x0 имеет предел, то этот предел единственный. Доказательство. Утверждение а) и б), вытекает прямо из соответствующих определений.
Предположим
противное, т.е. пусть в точке x0
функция
f(x)
имеет два предела y0
и y1,
и при этом y0
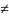 y1,
т.е. y0=
⇔
∀ε
> 0 ∃δ1
> 0 : ∀x
0 < |x − x0|
< δ1⇒
|f(x) − y0|
<
. и
y1=
⇔
∀ε
> 0 ∃δ2
> 0 : ∀x
0 < |x − x0|
< δ2⇒
|f(x) – y1|
<
.Тогда ∀x
∈
y1,
т.е. y0=
⇔
∀ε
> 0 ∃δ1
> 0 : ∀x
0 < |x − x0|
< δ1⇒
|f(x) − y0|
<
. и
y1=
⇔
∀ε
> 0 ∃δ2
> 0 : ∀x
0 < |x − x0|
< δ2⇒
|f(x) – y1|
<
.Тогда ∀x
∈
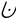 δ(x0),
где δ
= min{δ1,
δ2}
имеем 0
|y0
− y1|
|y0
− f(x)|
+ |f(x)
− y1|
<
+
δ(x0),
где δ
= min{δ1,
δ2}
имеем 0
|y0
− y1|
|y0
− f(x)|
+ |f(x)
− y1|
<
+
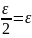 что противоречит предположению.
что противоречит предположению.
