8.Предел числовой последовательности и общие свойства предела.

Число a называется пределом последовательности (х_n), если для любого положительного числа ε найдется такое натуральное число n₀ = n₀(ε), что для всех n>n0 выполняется неравенство: |х_n-a|<ε . В этом случае говорят, что последовательность имеет предел и пишут 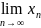=a.

можно записать более кратко:

Опр. Если существует число A и номер n0 ∈ N такие, что = A при любом n > n0, то последовательность { } будем называть финально постоянной. Опр. Последовательность { } называется ограниченной, если существует число M > 0 такое, что | |<= M при любом n ∈ N.

Теорема 1. а) Финально постоянная последовательность сходится; б) Если последовательность имеет предел, то он единственный; в) Сходящаяся последовательность ограничена.

Доказательство. а) Если = A при n > n0 ∈ N, то для любой окрестности V (A) точки A имеем ∈ V (A) при n > n0, т.е. =A; б)Положим N = max{N1,N2}. Тогда ∀ε > 0 ∀n > N будет справедливо | − a| < ε и |xn − b| < ε. Откуда|a − b| = |a − + − b| <= | − a| + | − b| < ε + ε = 2ε

т.е. 1/2|a − b| < ε для ∀ε > 0. Последнее возможно только при a = b. в) Пусть =a. Тогда по определению предела ( =a) ⇔ (∀ε > 0 ∃N ∈ N : ∀n > N ⇒ | − a| < ε), т.е. ∀n > N будет выполняться a − ε < xn < a + ε, а тем более −(|a| + ε) < < (|a|+ε). Пусть M = max{|x1|,|x2|,...,|xN|, |a| + ε}. Тогда получим, что | |<= M ∀n ∈ N.

9.Предельный переход и арифметические операции.

Если { }, {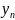 } - две числовые последовательности, то их суммой, произведением и частным на- зываются соответственно последовательности { + }, {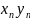 }, { / } (при делении предполагается, что все члены последовательности { } отличны то нуля). Теорема 2. Если последовательности { }, { } сходятся и lim 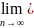= a, = b то: а) ( ± ) = ± = a ± b; б) c = c · = c · a, c ∈ R \ {0}; в) 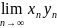= · = a · b; г) = 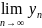= a b ( =/ 0, ∀n ∈ N; b =/ 0). Доказательство. Докажем случай г). Имеем ( = a ) ⇔ ( ∀ε > 0 ∃N1 ∈ N : ∀n > N1 ⇒ | − a| < ε) и ( = b) ⇔ ( ∀ε > 0 ∃N2 ∈ N : ∀n > N2 ⇒ | − b| < ε) . Поскольку b =/ 0, то ∃δ > 0 ∃N3 ∈ N : ∀n > N3 ⇒ | | > δ > 0. Пусть N = max{N1,N2,N3}. Тогда имеем в итоге

(∀ε1 > 0 ∃N ∈ N : ∀n > N ⇒ 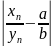< ε1) ⇔

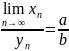
10.Предельный переход и неравенства.Если элементы сходящейся последовательности {x_n}, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).     Доказательство. Пусть все элементы x_n, по крайней мере начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {x_n}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |x_n - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < x_n - a < b - a. Используя правое из этих неравенств, получим x_n < b, а это противоречит условию теоремы. Случай x_n ≤ b рассматривается аналогично.