3.1. Методика определения коэффициентов критериального уравнения c использованием средств matlab
Для решения задачи обобщенной нелинейной регрессии в MATLAB имеется функция lsqnonlin(), возвращающая решение задачи нахождения точки минимума функции f(x)
(3.8)
где в общем случае f(x) – вектор-функция, х – вектор-столбец искомых переменных, L – некоторая константа.
Синтаксис функции lsqnonlin():
x = lsqnonlin(fun, x0)
x = lsqnonlin(fun, x0, lb, ub)
x = lsqnonlin(fun, x0, lb, ub, options)
x = lsqnonlin(fun, x0, lb, ub, options, P1, P2, … ),
здесь fun – название минимизируемой функции;
х0 – начальная точка, с которой начинается процесс поиска минимума функции;
lb, ub – соответственно левая и правая границы отрезка, на котором определяется минимум функции;
options – параметр, задающий режим работы функции оптимизирующей функции (перечень возможных значений данного параметра приведен в Help MATLAB в главе Optimization Toolbox в разделе Optimization Parameters);
P1, P2, … – параметры, от которых зависит функция fun.
Рассмотрим пример, демонстрирующий использование данной функции для нахождения коэффициентов функции при следующих значениях экспериментальных данных:
x (Re) |
1000 |
3000 |
5000 |
7000 |
9000 |
11000 |
13000 |
15000 |
y (Nu) |
10.16 |
24.42 |
29.56 |
33.15 |
34.57 |
21.2 |
19.81 |
2.21 |
М-файл:
function z=LR7_5(Coeff,vx,vy);
k=1:length(vx);
z=vy-(Coeff(1)*vx.^Coeff(2));
Текст программы:
function z= LR7_5 (Coeff,vx,vy);
x=[1000:2000:15000];
y=[10.16 24.42 29.56 33.15 34.57 21.2 19.81 2.21];
xi=[1000:10:15000];
z=[1 2];
Coeff = lsqnonlin(‘LR7_5’,z,[],[],[],x,y);
F=inline('b0*x.^b1','x','b0','b1')
yi=feval(F,xi,Coeff(1),Coeff(2));
plot(x, y, 'ko',xi, yi, 'k');
title('Аппрокcимация данных при помощи регреccии b0*x.^b1');
xlabel('\itx');
ylabel('\ity').
Coeff = 17.256 0.027224
3.2. Проверка адекватности полученных уравнений
Для оценки качества полученных критериальных уравнений необходимо использовать: 1) корреляционное отношение и 2) критерий Фишера.
Корреляционное отношение используется для оценки силы (тесноты) нелинейной связи (проведения корреляционного анализа):
,
(3.9)
где
f1=N–1,
f2=N–l
– числа степеней свободы; l
– число связей, наложенных на выборку
(для уравнения регрессии это число
определяемых коэффициентов
);
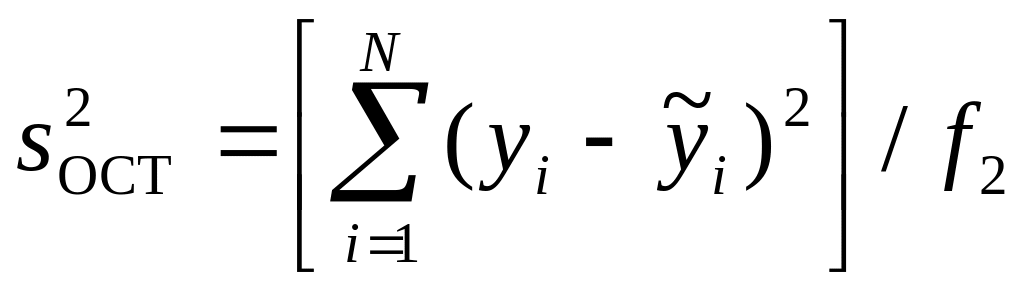– остаточная дисперсия;
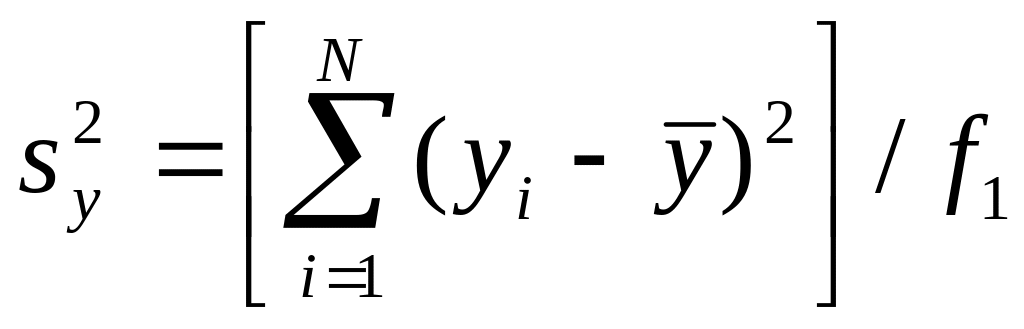– дисперсия относительно среднего.
Чем больше , тем сильнее связь (01). При =0 однозначное отсутствие связи между случайными величинами возможно только для нормального распределения. В случае линейной регрессии (l=2) корреляционное отношение равно коэффициенту корреляции =|r* |.
Критерий
Фишера F
используется для оценки качества
аппроксимации (проведение регрессионного
анализа).
При отсутствии параллельных опытов и,
следовательно, дисперсии воспроизводимости,
а также нормальном распределении
случайных величин yi
качество аппроксимации можно оценить
по
[1]. В данном случае он показывает, во
сколько раз уменьшается рассеяние
относительно полученного уравнения
регрессии по сравнению с рассеянием
относительно среднего. Чем больше
значение F
превышает табличное
(или f
– распределение в табл. 3.1) для выбранного
уровня вероятности (значимости,
надежности) p
(обычно
p=0.95)
и чисел
,
тем эффективнее уравнение регрессии.
Таблица 3.1
|
Степень
свободы
|
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
24 |
-- |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
161,4 |
199,5 |
215.7 |
224,6 |
230,2 |
234,0 |
238,9 |
243,9 |
249,0 |
254,3 |
2 |
18,51 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,37 |
19,41 |
19,46 |
19,50 |
3 |
10,13 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,84 |
8,74 |
8,64 |
8,53 |
4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,77 |
5,63 |
5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,53 |
4,36 |
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,84 |
3,67 |
7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,73 |
3,57 |
3,41 |
3,23 |
Окончание табл. 3.1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,12 |
2,93 |
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,23 |
3,07 |
2,90 |
2,71 |
10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,07 |
2,91 |
2,74 |
2,540 |
11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
2,95 |
2,79 |
2,61 |
2,40 |
12 |
4,75 |
3,88 |
3,49 |
3,26 |
3,11 |
3,00 |
2,85 |
2,69 |
2,50 |
2,30 |
13 |
4,67 |
3,80 |
3,41 |
3,18 |
3,02 |
2,92 |
2,77 |
2,60 |
2,42 |
2,21 |
14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,70 |
2,53 |
2,35 |
2,13 |
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,64 |
2,48 |
2,29 |
2,07 |