3.5. Метод Ньютона (метод касательных)

Графическая интерпретация метода представлена на рис.3.5. Предположим, что каким-либо способом найдено начальное приближение х₀ к истинному корню. Например, при использовании отделения корней, в качестве х₀ можно взять левую или правую границу промежутка, содержащего корень уравнения F(x) = 0, либо любую другую точку из этого промежутка. В точке х₀ вычислим значение функции F(x), а также значение ее производной F ^‘(x). Следующее приближение к корню, т.е. точку х₁ определим, как пересечение оси ОХ с касательной к кривой F(x) в точке х₀:

Аналогичным образом, вычислив значения F(x) и F ^‘(x), в точке х₁, можно получить приближение х₂:

В общем случае вычислительный процесс метода Ньютона выражается формулой:

(3.6)

где каждое новое значение х_k (k=1, 2, 3, …) будет располагаться все ближе к истинному корню х*., т.е. будет представлять собой все более точное приближение к решению уравнения F(x) = 0.

Рис.3.5. Метод Ньютона

Рис.3.6. Модифицированный метод Ньютона

Процесс уточнения корня по формуле (3.6) следует прекращать, когда выполнится условие , т.е. когда расстояние между двумя соседними приближениями станет меньше заранее за­данной точности .

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10^-5 – 10^-6 достигается за 4-5 итераций. Недостатком метода является необходимость вычисления на каждом шаге не только левой части F(x) уравнения, но и ее первой производной.

Алгоритм метода Ньютона представлен на рис. 3.7. Из формулы (3.6) видно что для вычисления каждого нового (текущего) приближения требуется знать лишь од­но предыдущее приближение. Эти две величины в блок-схеме названы соответственно хТ и хП. После ввода исходных данных переменной хП присваивается значение ( ) для того, чтобы первая проверка условия | хТ – хП | > обязательно дала значение True.

Рис.3.7. Алгоритм метода Ньютона

На практике иногда применяется так называемый модифицированный метод Ньютона, который отличается от метода Ньютона тем, что первая производная от F(x) вычисляется лишь один раз в точке х₀. Вычислительный процесс модифицированного метода Ньютона описывается формулой:

(3.7)

а его геометрическая иллюстрация приведена на рис. 3.6.

3.6. Метод простых итераций

Исходное уравнение (3.1) преобразуем к эквивалентному уравнению:

x = (x).

(3.8)

Пусть известно начальное приближение (полученное, например, на этапе отделения корней): x = x ₀. Подставим его в правую часть (3.8) и получим новое приближение: x₁ = (x₀). Повторяя эту процедуру, будем иметь в общем виде на некотором k-м шаге:

x_k = (x_k-1) .

В качестве условия окончания вычислительного процесса можно взять выполнение неравенства: x_k - x_k-1 < .

Значение x_k, удовлетворяющее ему, и есть корень уравнения (3.1).

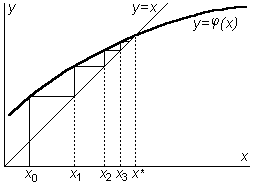
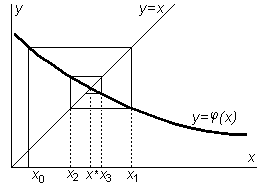
Геометрическая интерпретация этого метода приведена на рис.3.8, 3.9. Здесь x^* - истинное, искомое значение корня; x₀ - начальное приближение к корню; x₁, x₂, x₃ - оче­редные итерации.

Рис.3.8.

Рис.3.9.

При испо­ль­зовании этого метода возникает вопрос о его сходимос­ти. Дело в том, что при некоторых условиях расстояние между истинным корнем и прибли­жениями к нему может возрастать с каждой новой итерацией, как это показано на рис.3.10, 3.11.

Рис.3.10.

Рис.3.11.

Условием сходимости метода простых итераций является выполнение в окрестности искомого корня неравенства:

 (x) < 1

(3.9)

Это условие является достаточным, т.е. если оно выполняется, то процесс обязательно схо­­дится; если же условие (3.9) не выполняется или выполняется не во всех точках

x₀, x₁, x₂, ..., x_k, ... ,

то заранее сказать что-либо конкретное о сходимости нельзя.

Итак, для решения уравнения F(x) = 0 методом простых итераций надо преобразо­вать его к уравнению вида x = (x) так, чтобы выполнялось условие  (x) < 1. Схо­димость к истинному корню будет тем быстрее, чем ближе к единице значение (x).