Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
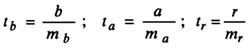
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
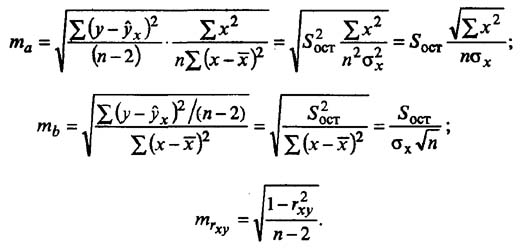
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
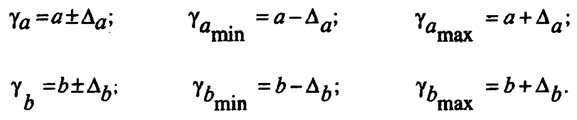
Прогнозное значение у определяется с помощью подстановки в уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
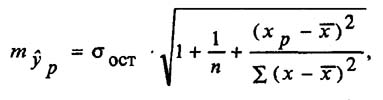
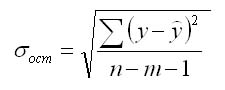
и находится доверительный интервал
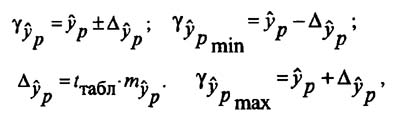
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
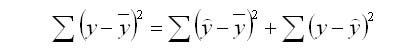
общая
сумма квадратов отклонений (TSS)
сумма
квадратов отклонений, обусловленная
регрессией (RSS)
остаточная
сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
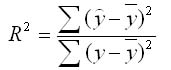
Любые задачи по эконометрике решаются здесь
Коэффициент детерминации - хаоактеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака. Соответственно величина 1-r^2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
Мультиколлинеарностью для линейной множественной регрессии называется наличие линейной зависимости между факторными переменными, включёнными в модель.
Мультиколлинеарность – нарушение одного из основных условий, лежащих в основе построения линейной модели множественной регрессии.
Мультиколлинеарность в матричном виде – это зависимость между столбцами матрицы факторных переменных Х
Гомоскедастичность - дисперсия каждого Еi одинакова для всех значений x.
При малом объеме выборки для оценки нарушения гомоскедастичности можно использовать метод Гольдфельда-Квандта, который включает:
1.Упорядочение наблюдений n по мере возрастания переменной х.
2. Исключения из рассмотрения центральных наблюдений C; (n-C)/p при этом где p – число оцениваемых параметров.
3. Разделение совокупности (n-C) на две группы (с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.
4. Определение остаточной суммы квадратов для обеих групп (S1) и (S2) и нахождение их отношения: R=S1/S2 При выполнении нулевой гипотезы о гомоскедастичности отношение R будет соответствовать F-критерию с (n-C-2p)/2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табл. значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.