
5.5. Дифракция звука на мягкой сфере,
расположенной в твёрдом теле.
Поскольку излучение в твёрдое тело имеет свои особенности, связанные с наличием сдвиговой упругости, дифракция звука также должна иметь особенности в частотной зависимости эффективности рассеяния на низких частотах.
Рассмотрим для примера рассеяние продольной волны мягкой сферой. Задача формулируется следующим образом:
![]() ,
,
,
![]() .
.
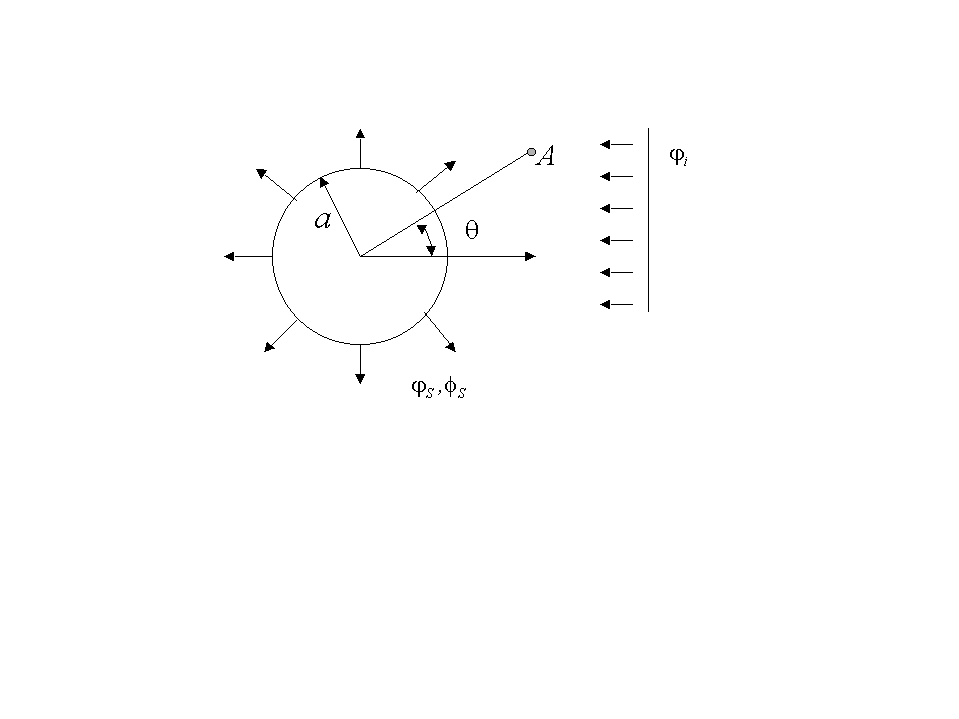
Здесь, как и в задаче на излучение в твёрдое тело зонального источника, векторный потенциал рассеянной волны имеет только одну угловую компоненту:
![]() ,
,
![]() ,
,
![]() ,
,
Разложим падающую продольную волну в ряд по сферическим волнам и воспользуемся представлением поля зонального источника в твёрдом теле (3.7.):
![]() ,
,
![]() ,
,
![]() .
.
Подставляя
решение в граничные условия, получаем
исходную систему уравнений для определения
набора постоянных
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
мощность, переносимая падающей
волной через сечение сферы. Отдельные
составляющие коэффициента
![]() имеют следующие низкочастотные оценки:
имеют следующие низкочастотные оценки:
![]() ,
,
 ,
,
причём первое слагаемое соответствует ненаправленному излучению продольной волны, второе – дипольному излучению продольной волны (ось диполя совпадает с направлением падающей волны) и дипольному излучению поперечной составляющей в перпендикулярной плоскости. Вкладом квадрупольной составляющей на низких частотах можно пренебречь.
Можно отметить,
что по типу частотной зависимости
рассеяния на низких частотах мягкий
рассеиватель в твёрдом теле является
аналогом жёсткого в жидкости и наоборот.
Сравнительные энергетические
характеристики излучения сферой и
рассеяния на сфере на низких частотах
сведены в таблицу для монополя, диполя,
квадруполя (![]() соответственно,
соответственно,
![]() ).
).
|
жидкость |
тв. тело |
|
||||
|
0 |
1 |
2 |
0 |
1 |
2 |
|
|
|
|
|
|
|
|
излучение |
|
|
|
|
|
|
|
|
мягкая сфера |
|
|
|
|
|
|
Рассеяние |
жёсткая сфера |
|
|
|
|
|
|
|
ЛИТЕРАТУРА
Основная
Лепендин Л.Ф. Акустика. Учебное пособие, М. Высшая школа, 1978г.
Исакович М.А. Общая акустика. Учебное пособие, М. Наука, 1973г.
Ржевкин С.Н. Курс лекций по теории звука, МГУ, 1980г.
Горелик Г.С. Колебания и волны. Физматгиз, 1959г.
Дополнительная
Стретт Д.В. (лорд Релей) Теория звука, т.1,2, ГИТТЛ, 1955г.
Скучик Е. Основы акустики, т.1,2, ИЛ. 1958г., МИР, 1976г.
Бреховских Л.М. Волны в слоистых средах, М, Наука, 1957г., 1973г.
Шендеров Е.Л. Волновые задачи гидроакустики, Л. Судостроение, 1972г.
Шендеров Е.Л. Излучение и рассеяние звука, Л. Судостроение, 1989г.
Морз Ф. Колебания и звук, ГИТТЛ, 1949г.
Зоммерфельд А. Механика деформируемых сред, ИЛ, Москва, 1954г.
Гринченко В.Т., Мелешко В.В. Гармонические колебания и волны в упругих телах, Киев, Наукова думка, 1981г.
Викторов И.Л. Физические основы применения ультразвуковых волн Релея и Лэмба в технике, М. Наука, 1960г.
Пузырёв Н.Н. Методы сейсмических колебаний, Новосибирск, Наука, 1992г.
Фёдоров Ф.И. Теория упругих волн в кристаллах, М., Наука, 1965г.
Кольский Г. Волны напряжения в твёрдых телах, ИЛ, 1955г.
Зарембо Л.К., Красильников В.А. Введение в нелинейную акустику, М, Наука, 1966г.
Новиков Б.К., Руденко В.В., Тимошенко В.И. Нелинейная гидроакустика, Л. Судостроение, 1981г.
Наугольных К.А., Островский Л.А., Нелинейные волновые процессы в акустике, М., МИР, 1990г.
Физическая акустика, под ред. Мэзона тт.19, 19661976гг.
Библиотека инженера гидроакустика, Л. Судостроение, 19761996гг. (~50 книг)
Слепян Л.И. Нестационарные упругие волны, Л. Судостроение, 1972г.
Л. Бергман Ультразвук, ИЛ, М., 1957г.
Э. Госсард, У. Хук Волны в атмосфере, М., МИР, 1978г.
Стокер Д.Д. Волны на воде, ИЛ. Москва, 1958г.
С.Б. Бирюков, Ю.В. Гуляев Поверхностные акустические волны в неоднородных средах, М., Наука, 1991г.
Расчёт сферического излучателея.
Методические указания к курсовому проектированию по курсу
«Общая акустика» для студентов
специальности 1904.
Цель курсового проектирования – закрепления теоретических сведений, полученных на лекциях, и их применение для расчёта конкретных излучателей, которые можно описать в рамках модельного сферического излучателя как наиболее близкого к реальным излучателям. Основные теоретические сведения содержатся в курсе лекций «Общая акустика», в настоящем методическом пособии приведены лишь расчётные формулы с краткими пояснениями.
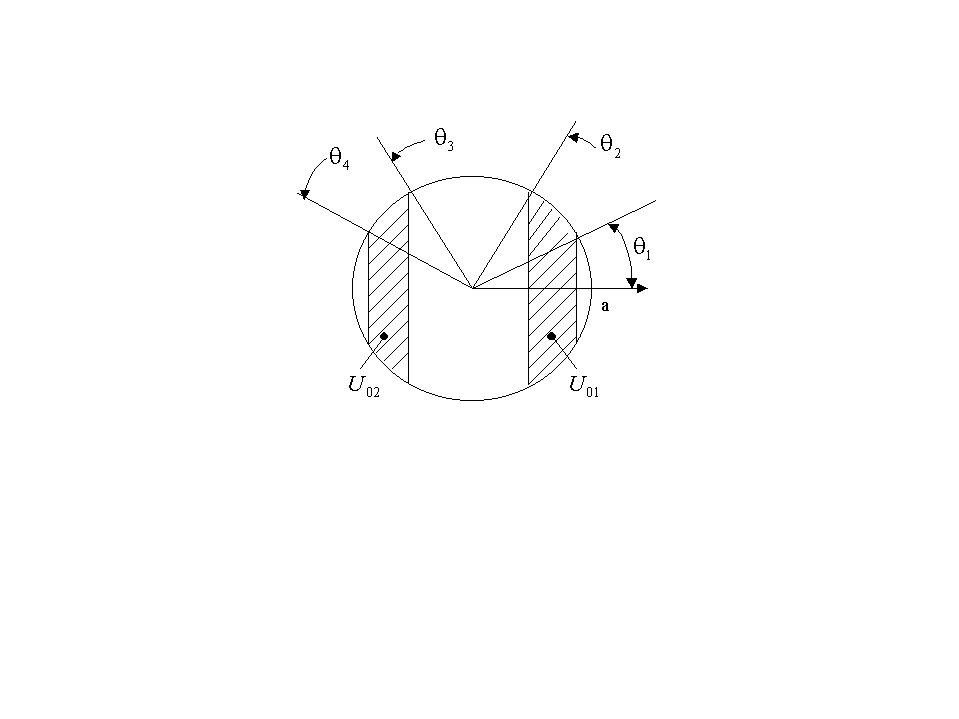
Матрица заданий содержит 10 вариантов углового распределения амплитуды колебательной скорости по поверхности излучателя и 3 варианта амплитудно-фазового распределения, которым соответствуют симметричное распределение (I вариант), антисимметричное распределение (II вариант) и асимметричное распределение (III вариант).
При симметричном распределении колебательной скорости излучатель ведёт себя на низких частотах как монопольный излучатель, при антисимметричном распределении – как дипольный излучатель, при асимметричном распределении – как излучатель, поле которого можно найти как полусумму полей, создаваемых излучателями симметричного и антисимметричного типов, причём такое разложение справедливо на любых частотах.
Изменяя рабочую частоту в широких пределах студенты должны самостоятельно проконтролировать свои расчёты и свои знания основных закономерностей излучения в предельных случаях низких и высоких частот.
Пояснительная записка, кроме основных сведений из теории излучения, должна содержать раздел «Выводы» с кратким анализом полученных результатов, а также их соответствия теоретическим в предельных случаях низких и высоких частот.
Основные расчётные формулы.
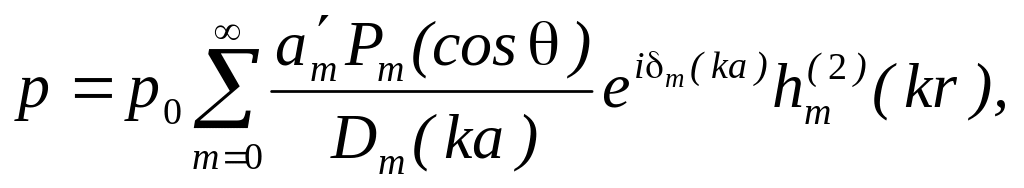 звуковое
давление
звуковое
давление
 .
.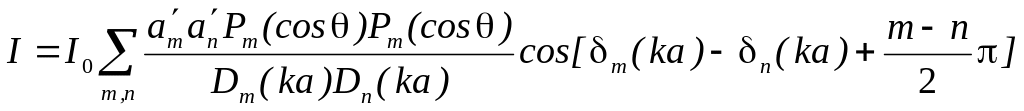 -
интенсивность звука,
-
интенсивность звука,
 .
. -
акустическая мощность,
-
акустическая мощность,
 .
.
3.1. ![]() -
нормированное активное сопротивление
(метод дальнего поля).
-
нормированное активное сопротивление
(метод дальнего поля).
3.2. ![]() -
нормированное активное сопротивление
(метод ближнего поля).
-
нормированное активное сопротивление
(метод ближнего поля).
 -
нормированное реактивное сопротивление.
-
нормированное реактивное сопротивление. -
характеристика направленности (ХН),
-
характеристика направленности (ХН),
 -
направление максимума ХН.
-
направление максимума ХН. -
коэффициент осевой концентрации.
-
коэффициент осевой концентрации.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
I вариант (симметричное распределение).
![]() ,
,
![]()
![]() ,
,
II вариант (антисимметричное распределение).
![]() ,
,
![]() ,
,
III вариант (асимметричное распределение).
![]() .
.
 I
вариант:
I
вариант:
![]()
II
вариант:
![]()
III
вариант:
![]()
Матрица заданий.
N |
Варианты углового распределения |
Варианты амплитудно- фазового распределения |
|
|
|
|||||
|
|
|
|
I |
II |
III |
||||
1 |
0 |
10 |
170 |
180 |
1 |
2 |
3 |
0,5 |
|
100 |
2 |
0 |
20 |
160 |
180 |
4 |
5 |
6 |
|||
3 |
0 |
30 |
150 |
180 |
7 |
8 |
9 |
|||
4 |
20 |
30 |
150 |
160 |
10 |
11 |
12 |
|||
5 |
20 |
40 |
140 |
160 |
13 |
14 |
15 |
|||
6 |
20 |
50 |
130 |
160 |
16 |
17 |
18 |
|||
7 |
40 |
70 |
110 |
140 |
19 |
20 |
21 |
|||
8 |
50 |
80 |
100 |
130 |
22 |
23 |
24 |
|||
9 |
60 |
90 |
90 |
120 |
25 |
26 |
27 |
|||
10 |
70 |
90 |
90 |
110 |
28 |
29 |
30 |
|||
Диапазон
частот
![]() кГц.
кГц.
Характеристика направленности и коэффициент осевой концентрации вычисляются для частот:
![]() кГц,
кГц,
остальные
характеристики рассчитываются во всём
диапазоне частот
![]() .
Интенсивность звука и звуковое давление
вычисляются для
.
Интенсивность звука и звуковое давление
вычисляются для
![]() ,
,
![]() (I
вариант),
(I
вариант),
![]() -
для II и III
вариантов.
-
для II и III
вариантов.
Графический материал.
Характеристики направленности для частот кГц.
Частотные характеристики для величин
 в диапазоне
в диапазоне
 и
и
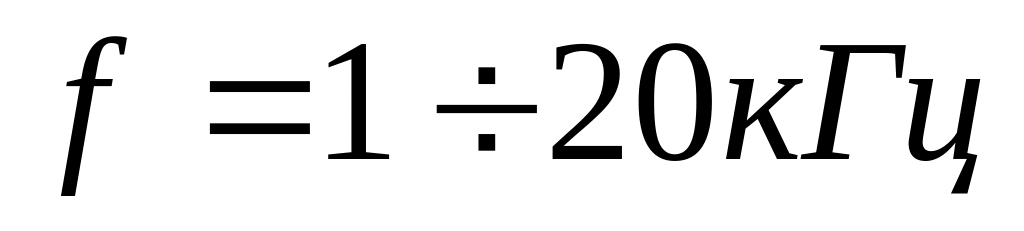 на отдельных рисунках.
на отдельных рисунках.
Табличный материал.
Таблицы
значений
![]() с указанием размерности.
с указанием размерности.
