
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:белеты.docx
X
- •1.Единственность решения задачи Коши Теорема:
- •2.Непрерывная зависимость решения
- •3.Существование производной по параметру для решения з. Коши
- •4.∃ И ед. Решения з. Коши n-го п-ка на отр.
- •6. Ед. Решения з. Коши норм. Системы
- •7.Устойчивость по первому приближению
- •8. Определение непр. Зависимости решения з.Коши от начального усл.
- •29. Сформулировать и доказать теорему о существовании общего интеграла у дифференциального уравнения в полных дифференциалах.
- •32.Опишите процедуру исследования решения системы обыкновенных дифференциальных уравнений на устойчивость по первому приближению.
- •43.Дать определение асимптотической устойчивости решения нормальной системы дифференциальных уравнений.
- •47.Дать определение устойчивости по Ляпунову для нулевого решения нормальной системы дифференциальных уравнений.
- •49.Дать определение общего интеграла и общего решения обыкновенного дифференциального уравнения 1-го порядка.
- •51.Сформулировать и доказать теорему об устойчивости по Ляпунову для линейной системы дифференциальных уравнений с постоянными коэффициентами.
- •58.Какие условия должны быть выполнены, чтобы задача Коши была корректной по Адамару?
58.Какие условия должны быть выполнены, чтобы задача Коши была корректной по Адамару?
Постановка задачи Коши называется корректной по Адамару, если в ней заданы такие условия, что существует единственное решение задачи, устойчивое к малым изменениям. Это значит, что постановка задачи обеспечивает существование и единственность решения, которое должно быть устойчивым по отношению к изменениям правой части и начальных данных.
Формулировка устойчивости решения:
для ∀ε>0 ∃δ>0:
из |f1-f2|<δ
и |y01-y02|<δ
⇒ |y1-y2|<ε,
где
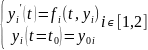
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
