1.Единственность решения задачи Коши Теорема:

Решение задачи Коши

{ y’(t)=f(t,y), t∊[t₀,t₀+T]

{ y(t₀)=y₀

Для ДУ 1-го порядка, разрешённого отн. произв., единственно, если:

1)f(t,y) непр. по t и y в области

R: t₀<t<t₀+T ; y₀-b<y<y₀+b ;

2)f(t,y) удовл. в области R усл. Липшица по y:

|f(t,y1)-f(t,y2)|≤N|y1-y2|,y1,y2∊f[y0-b; y0+b]

Д-во:

Необх. д-ть единственность решения задачи Коши при вып. усл. данной теоремы. Редуцируем задачу Коши в предположение сущ. решения к интегральному уравнению y(t)=y₀+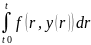

предположим, оно имеет 2 решения y₁(t) и y₂(t).

Тогда их разность u(t)=y₁(t)-y₂(t) удовл., согласно инт. ур., интегральному соотношению

{ u(t)= 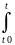(f(r,y₁(t))-f(r,y₂(t)))dr

{ y(t₀)=0

Сделаем оценку u(t), используя усл. Липшица

|f(r,y₁)-f(r,y₂)|≤N|u(r)|

Тогда |u(r)|≤ |f(r,y1)-

-f(r,y2)|dr≤N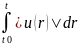 при t₀<t<t₀+ε

где ε выбирается так,чтобы |y_m(t)-y₀|≤b,m=1,2

и, следовательно, можно использовать усл. Липшица. Т.к. N=const, то по лемме Грануолла-Беллмана, при g(t)=0 имеем 0≤u(t)≤0⇒u(t)=0⇒y₁=y₂ ∎

2.Непрерывная зависимость решения

Теорема:

Если в задаче Коши

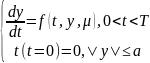
f(t,y,μ) непр. по всем аргументам в области

D:{0≤t≤T, |y|≤a, |μ-μ₀|≤b} и

удовлетворяет по перем. y условию Липшица

|f(t,y₁,μ)-f(t,y₂,μ)|≤k|y₁-y₂|

всюду в D, причём k не зависит от t и μ, то решение задачи y=y(t,μ) определено в D и непрерывно по t и μ.

3.Существование производной по параметру для решения з. Коши

Теорема

Q_μ={(t,y,μ): |t=t_o|≤T, A≤y≤B, μ₁≤μ≤μ₂}

Теорема

Пусть функция f(t,y,μ) непр. в Q_μ и имеет в Q_μ непр. частные производные f_y(t,y,μ), f_μ(t,y,μ), а ф-ия y_o(μ) непр. диф. на отрезке [μ₁,μ₂]. Тогда, если y(t,μ) – решение задачи Коши

а) y’(t)=f(t,y(t),μ), t∊[t_o-T,t_o+T]

б) y(t_o)=y_o(μ)

на отрезке [t_o-T,t_o+T] для всех μ∊[μ₁,μ₂], то ф-ия y(t,μ) имеет при t∊[t_o-T,t_o+T] μ∊[μ₁,μ₂] произв. по μ

Д-во

Пусть μ и μ+Δμ – 2 произв. точки отрезка [μ₁,μ₂]. Рассм. соотв. этим параметрам решения задачи Коши y(t,μ) И y(t ,μ+Δμ). Определим ф-ию

v(t,μ,Δμ)=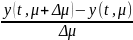 ,t∊[t_o-T,t_o+T]

т.к. ф-ции y(t,μ+Δμ), y(t,μ) явл. решениями ур. а) на отр. [t_o-T,t_o+T] при соотв. значениях параметров, то

v’(t,μ,Δμ)= *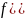

Преобразим выражение, стоящее справа:

* =

Применяя формулу конечных приращений

f(t,y₁)-f(t,y₂)=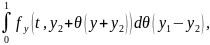 получим

=

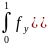
Введём ф-ии p(t,μ,Δμ)=

q(t,μ,Δμ)=

v’(t,μ,Δμ)=p(t,μ,Δμ)*v(t,μ,Δμ)+q(t,μ,Δμ)**

⇒v явл. решением лин. ДУ первого порядка на отр. [t_o-T,t_o+T]

Из определения v(t,μ,Δμ) следует, что она удовл. начальному усл. v(t,μ,Δμ)= ⦁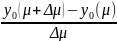

Решение задачи Коши а),б) имеет вид

v(t,μ,Δμ)=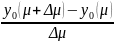 exp{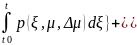

t∊[t_o-T,t_o+T] ⦁⦁

Для д-ва ∃ произв. 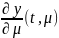достаточно д-ть, то ф-ия v(t,μ,Δμ) имеет предел при Δμ 0. Покажем, что ∃ предел правой части ф-лы ⦁⦁ при Δμ 0

т.к. ф-ия y_o(μ) непр. диф., то

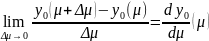
Найдём предел ф-ии p(t,μ,Δμ) при Δμ 0. Из непрерывности в Q_μ частной пр. f_y(t,y,μ) и опр. ф-ии p(t,μ,Δμ) следует, что

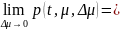
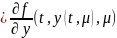равномерно по (t,μ)∊[t_o-T,t_o+T]X[μ₁,μ₂]. Из существования частной пр. f_μ(t,y,μ) имеем равномерно по (t,μ)∊[t_o-T,t_o+T]X[μ₁,μ₂]. Следовательно, предел правой части формулы ⦁⦁ существует, и переходя в этой формуле к пределу при Δμ 0, получим

∎