4. Примеры проявления силы Кориолиса. Лагранжево описание движения

Круг инерции. Придадим частице воды некоторую начальную скорость и рассмотрим изменение скорости этой частицы под действием ускорения Кориолиса и при отсутствии трения. Описание движения, привязанное к движущейся частице, называется лагранжевым, а к неподвижной точке поля – эйлеровым. Возмем исходные уравнения

. (5.4.1)

Интегрируя, получим

(5.4.2)

Делим на f, возводим в квадрат и складываем, вводя вектор скорости ,

. (5.4.3)

Сравним (5.4.3) с уравнением окружности, где R – радиус окружности,

. (5.4.4)

Положим координаты центра окружности равными

.

Получается, что численно равно радиусу окружности. Он называется радиусом круга инерции

. (5.4.5)

Это же равенство можно записать иначе, умножив на V

(5.4.6)

В левой части уравнения стоит ускорение Кориолиса, в правой – центробежная сила. Период обращения частицы по кругу инерции τ получим, разделив длину окружности 2R на скорость

(5.4.7)

Этот период равен половине маятниковых суток (2/sin). Величина τ зависит от широты места следующим образом: при  = 0; 10; 30; 50; 70; 90^о  = ∞; 61,1; 24,0; 15,7; 12,8; 12,0 ч.

Величина круга инерции в высоких и средних широтах очень невелика. Так в среднем течении Гольфстрима при V = 1 мс^–1, f = 10^–4 c^–1 R = 10 км. Уравнение круга инерции было получено в 1852 г. Уильямом Феррелем.

Экмановская циклоида. Уравнения градиентного неустановившегося течения

(5.4.8)

запишем в виде, удобном для лагранжева описания движения с градиентом давления по оси х

. (5.4.9)

Будем рассматривать движение жидкой частицы без трения под действием постоянной силы градиента давления и силы Кориолиса. Умножим первое уравнение (5.4.9) на и сложим со вторым уравнением (5.4.9)

. (5.4.10)

Потребуем, чтобы , где r – произвольная величина. Подставим в (5.4.10)

. (5.4.11)

Определим r так, чтобы . Из этого равенства при f = const получаем

. (5.4.12)

и из (5.4.11) . Следовательно

. (5.4.13)

Интегрируем, полагая что есть постоянная движущая сила на единицу массы,

. (5.4.14)

Положим C₂ = C/C₁ и умножим на значение r (5.4.12)

. (5.4.15)

Примем начальное условие v + ui = 0 при t = 0. Откуда

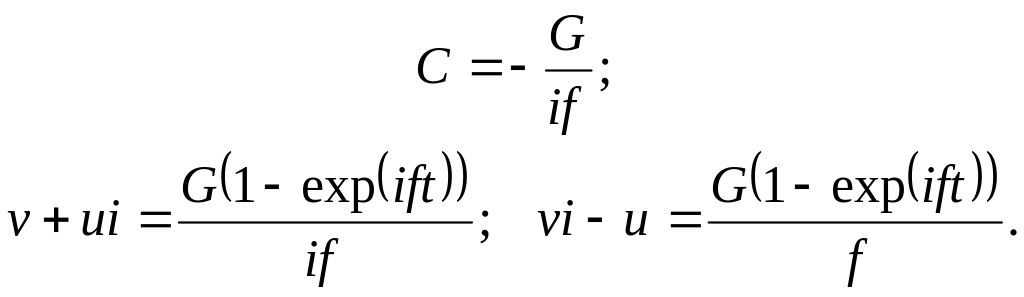(5.4.16)

Используя формулу Эйлера , получим выражение комплексной скорости и составляющих по осям координат

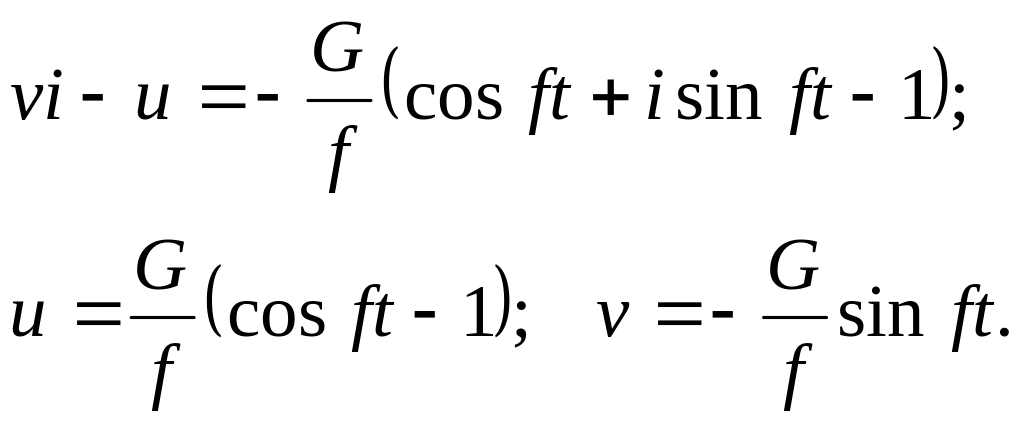(5.4.17)

Ищем траекторию движения частицы. Записываем скорости через производные dx/dt, dy/dt и интегрируем, обозначая начало движения через x₀, y₀

. (5.4.18)

Мы получили уравнение движения по циклоиде, опубликованное Экманом в 1905 г. Отметим некоторые параметры этого уравнения. Высота циклоиды может рассматриваться как некоторый масштаб локализации, ограничивающий передвижение частицы в направлении движущей силы. Длина базиса циклоиды . Длина ветви . Период прохождения одной ветви равен половине маятниковых суток . Средняя скорость движения перпендикулярно движущей силе G равна скорости геострофического течения . Максимальная скорость достигается в вершине циклоиды и равна , максимальная скорость в направлении градиента равна геострофической и достигается на половине высоты циклоиды.

Приведенное решение при переменных значениях параметра Кориолиса f и градиента давления применялось для расчета траекторий частиц в антипассате (рис. 5.4.1), а также при переменном градиенте давления для анализа движений поплавков нейтральной плавучести (рис. 5.4.2) и расшифровки записи самописцев течений.

Рис. 5.4.1 Траектория движения частиц в антипассате

Сплошные линии – наблюдения, пунктирные – расчет по формулам (5.4.9) от начала движения до вершины циклоиды (В. Л. Лебедев, 1974)

Когда градиент давления в процессе движения уменьшается или возрастает сила Кориолиса, базис циклоиды будет укорачиваться, и частицы начнут описывать инерционные петли. На рис. 5.4.2 показаны петли дрейфующего поплавка нейтральной плавучести в районе глубинного противотечения Куросио. Рядом нанесена расчетная траектория, полученная при уменьшении градиента давления по закону , где а – коэффициент, уменьшающий величину градиент в сто раз за два месяца дрейфа.

Рис 5.4.2 Циклоидальные траектории

Сплошная линия – путь поплавка нейтральной плавучести на горизонте 1000 м, точки – вычисленная траектория, цифры – время. (В. Л. Лебедев, 1984)