Глава 12. Модели полных потоков, суммарной и внутренней циркуляции

1. Суммарная циркуляция по балансу Свердрупа

Карта глобальной циркуляции в полных потоках, основанная на формулах свердруповского баланса с дополнением данных по антарктическому кольцу (рис. 12.1.1) была составлена В. А. Бурковым и А. И. Харламовым (Бурков, 1980).

Рис.12.1.1 Средний многолетний результирующий перенос вод в Мировом океане по свердруповскому балансу и по измерениям в антарктическом кольце.

1 – изолинии функции переноса (разность между цифрами на линиях дает расход в свердрупах (10⁶м³с^–1)); 2 – оси циклонических круговоротов; 3 – оси антициклонических круговоротов

Согласно формуле свердруповского баланса (11.7.4), широтная составляющая полного потока вычисляется от нулевого значения на восточных берегах океана. Поэтому расчет по свердруповскому балансу в антарктическом кольце невозможен. Циркуляция для этих вод была построена на основе инструментальных наблюдений (общий расход в проливе Дрейка) и поля плотности (распределение общего расхода).

В районе западных пограничных течений свердруповский баланс напрямую не работает, и там были приняты расходы, замыкающие баланс вод в круговых циркуляциях. Комментируя карту, Бурков пишет, что циркуляция «удивительным образом хорошо согласуется с поверхностной циркуляцией, построенной по наблюдениям», отражает западную интенсификацию, асимметрию круговоротов и межпассатные противотечения (с. 31).

Свердруповский перенос Бурков называет ветровым и считает, что его глубина ограничена бароклинным слоем 1000–1500 м. Надо иметь в виду, что под ветровыми течениями Бурков понимает «результирующие течения, включающие как дрейфовые, так и градиентные составляющие» (Бурков, 1980, с.17). Свердруповский баланс масс складывается из дивергенций двух течений: геострофического и дрейфового.

Помимо среднегодового значения свердруповской циркуляции Бурков приводит ее сезонные колебания. Для Гольфстрима это среднегодовой расход 53 св, зимний 81, весенний 36, летний 37, осенний 57.

Группа океанологов с участием Г. Стоммела писала: «Мы заключаем, что есть хорошие основания полагать, что внутренний (бароклинный – В. Л.) перенос в субтропическом круговороте Северной Атлантики существенно согласуется со свердруповским соотношением вихря ветрового трения».¹³

2. Модели Стоммела (1948) и Манка (1950)

Модели Стоммела и Манка стали важными шагами в развитии свердруповской идеи вихревого баланса путем включения в этот баланс новых источников завихренности в виде трения. Кроме того, теоретическая модель Стоммела дала первое объяснение восточно-западной асимметрии поверхностной циркуляции. Асимметрия эта выражается западной интенсификацией течений и проявляется даже при самых простых условиях моделирования.

Модель Стоммела. Стоммел рассмотрел циркуляцию в замкнутом прямоугольном, однородном бассейне с плоскими дном. Ветровые условия упрощенно повторяли область субтропического круговорота в Северной Атлантике. На рис. 12.2.1 а показана форма бассейна и распределения: трения ветра, составляющих свердруповского потока по меридиану и параллели, а также решение, найденное Стоммелом (б).

Рис. 12.2.1. Проблема циркуляции у западного берега в рамках свердруповской модели (а) и ее решение Стоммелом за счет вихря донного трения (б). 1 – западный пограничный слой, где свердруповский баланс не пригоден; 2 – составляющие полного переноса по свердруповскому балансу; 3 – распределение ветра над акваторией; (б) – изолинии функции переноса по модели Стоммела

В рамках свердруповской модели субтропический круговорот не замыкается у западного берега. Модель требует здесь, как и везде, дать течению южную составляющую из-за антициклонической завихренности. В этом месте его можно замкнуть, игнорируя модель и исходя из условия баланса воды воль линий тока или дополнив модель новым вихрем циклонического знака. Он должен резко обостриться в западной прибрежной зоне и подавить антициклонический вихрь трения ветра.

В виде источника такого вихря Стоммел выбрал трение о дно, приняв его по величине пропорциональным скорости течения, а по направлению – обратным скорости. Из рисунка 12.2.1 понятно, что такой вихрь изначально будет циклоническим (обратным скорости) и что он преодолеет вихрь трения ветра в случае очень быстрого и узкого течения у берега и баротропности модели океана, при которой скорость, не затухая, доходит до дна.

Исходные уравнения

. (12.2.1)

Граничные условия:

при z = h (морская поверхность) , (12.2.2)

где b – меридиональная протяженность бассейна;

при (дно) . (12.2.3)

Условие на берегу – непротекание и скольжение, выражено равенством нулю функции тока . Изолинии  выражают суммарный расход

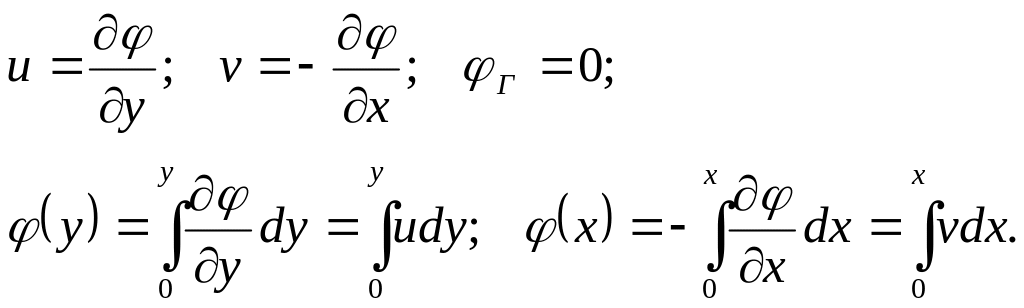(12.2.4)

Уравнения (12.2.1) интегрируются от дна до поверхности, перекрестно дифференцируются и складываются. Получается

. (12.2.5)

Это равносильно свердруповскому балансу с добавкой вихря придонного трения

. (12.2.6)

Уравнение (12.2.5) решается с помощью разделения переменных по методу Фурье. Основной результат в виде изолиний функции переноса  с нанесенными на них расходами показан на рис. 12.2.1 (6). Напомним, что изолинии функции переноса являются одновременно и линиями тока. Параметр Кориолиса представлен линейной функцией широты.

Стоммел провел на этой модели эксперименты, показавшие, что без учета изменения параметра Кориолиса с широтой западная интенсификация течений не происходит. Очевидно, что при этом неосуществим и свердруповский баланс.

Модель Манка. Блестящее решение Стоммела отделяет от реального океана пропасть, вызванная тем, что Гольфстрим не испытывает существенного донного трения и даже не везде достигает дна. Эту пропасть перешагнул Манк, заменив донное трение боковым. Кроме того, Манк значительно приблизил к реальности поле трения ветра, представив его в виде суперпозиции гармонических функций.

В аналитической модели Манка используются установившиеся полные потоки, плоская нижняя граница без трения и постоянное значение . Условие баротропности нигде не вводится и, по мнению Лакомба, модель Манка можно считать бароклинной по умолчанию. Приближение к ровному дну в реальном океане возможно только за счет бароклинности.

Исходные уравнения в модели Манка имеют вид

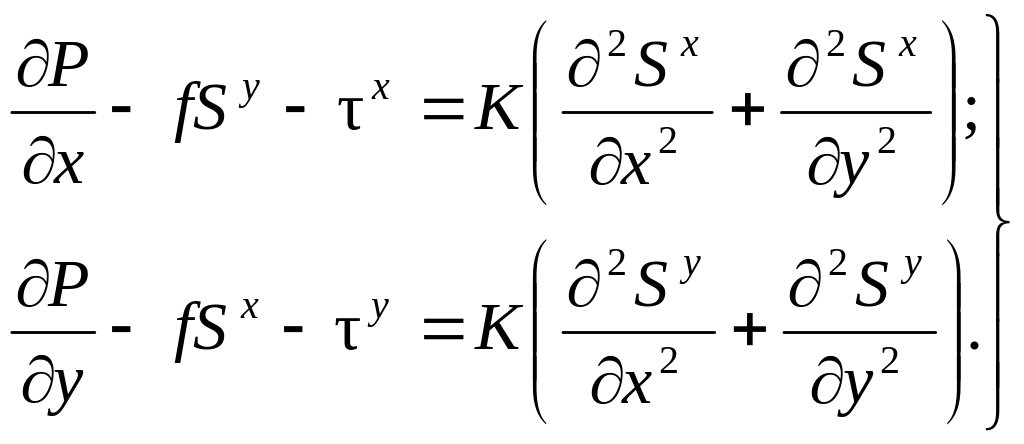(12.2.7)

где P – интеграл по глубине от давления, S – полный поток массы, правые части уравнений выражают боковое трение по осям x и y – R_x и R_y

Перекрестным интегрированием и вычитанием уравнение баланса завихренности Манк получает

или , (12.2.8)

где  – ротор бокового трения, ,  – функция полного потока.

Условие на береговой границе состояли в непротекании (функция переноса  = 0 совпадает с границей) и прилипании (нормальные к границе производные  равны нулю: ∂/∂n = 0).

Были получены решения в условиях разного приближения к реальности. Наиболее интересными оказались расходы вдоль поперечного сечения Гольфстрима. На них с мористой стороны явно обозначилось противотечение.

Это связано с заданием бокового трения в исходных уравнениях (12.2.7). При такой записи ротор трения на мористом краю Гольфстрима получает отрицательный знак, совпадающий со знаком ротора трения ветра. По условию баланса массы это должно вызывать боковое противотечение на юг. Оно действительно наблюдается в океане и составляет по расчетам Манка 17% расхода течения. На этом основании Манк уточнил расход Гольфстрима через замыкания водного баланса в круговой циркуляции в виде формулы

, (12.2.9)

где L – ширина океана.

Расход на 35^ос. ш. получился равным 36 св.

На рис. 12.2.2 показаны в условном масштабе изменения с удалением от американского берега на восток интегрального расхода север–юг и величина полного потока.

Рис.12.2.2. Интегральный расход X и полный поток в условном масштабе по модели Манка на поперечном разрезе западного пограничного течения (  – линейный масштаб) (Г. Стоммел, 1963)

Ширина течения регулируется в модели подбором коэффициента боковой вязкости. Вычисления проводятся по формуле, получившей в океанической литературе название «ширины слоя Манка»

. (12.2.10)

При K = 5∙10⁷ см² с^–1 Манк получил ширину течения 200 км, при K = 10⁶ см² с^–1 ширина потока будет около 50 км, расход останется прежним.