4. Эпюра градиентного течения над дном

В структуре градиентного течения у дна выделяется придонная экмановская спираль левого разворота (в поверхностном слое трения экмановская спираль имеет правый разворот); у дна спираль завершается логарифмическим слоем почти прямолинейного движения, где сила Кориолиса подавлена трением (рис. 10.9.1).

Эта модель опубликована Экманом в 1905 г. и для глубокой воды идентична по графическому изображению более поздней спирали Акерблома (1908) и атмосферной спирали Тейлора (1916). Экман указывал, что его спираль пригодна и для атмосферы.

Рис. 10.9.1. Придонные спирали Экмана (1905) для градиентных течений мелкого и глубокого моря

Математическое описание спирали у Экмана рассчитано на универсальное решение для глубокого и для мелкого моря. Поэтому в учебной литературе используется более простой вариант решения – решение для глубокого моря. В исходных уравнениях присутствует и трение, и градиент давления

, (10.9.1)

где  – удельный объем; нижние индексы означают дифференцирование.

Умножим второе уравнение (10.9.1) на мнимую единицу и сложим уравнения (10.9.1)

(10.9.2)

где М – комплексная скорость.

Разделим (10.9.2) на if , примем обозначение и заменим градиент давления по формуле геострофического течения fu_g = –p_y

. (10.9.3)

Решение неоднородного уравнения (10.9.3) проведем по схеме

M_он (общ. неодн. ур.)  = M_чн (частн. неодн. ур.) + M_оо (общ. однор. ур.).

Примем

. (10.9.4)

Представим (10.9.3) в виде общего однородного уравнения и запишем его решение

; (10.9.5)

. (10.9.6)

При удалении от дна скорость не должна возрастать безгранично, поэтому C₁ =0

. (10.9.7)

При z = 0 (дно) M = 0, C₂  = –u_g.

Окончательно получаем

. (10.9.8)

Подставляем ,

; (10.9.9)

, (10.9.10)

где D – глубина трения.

Полный перенос в слое придонного трения распределен между двумя осями таким образом

; (10.9.11)

. (10.9.12)

При h > D полный перенос в направлении градиента давления n равен

. (10.9.13)

Придонная скорость отклоняется от градиента давления в северном полушарии на 45^о вправо, обращаясь в пределе в нуль.

Существует интересная связь между двумя экмановскими спиралями – дрейфовой и придонной. Если использовать подвижную систему координат, соединив ее с концом вектора поверхностной скорости, то, проведя стрелки от конца этого вектора на концы остальных, заглубленных, векторов скорости, получим спираль экмановского придонного течения (см. рис. 10.9.2).

Рис. 10.9.2. Взаимная обратимость дрейфовой и придонной экмановских спиралей.

Взаимная обратимость двух спиралей была выражена математически С. С. Зилитинкевичем ⁹ и использована для того, чтобы применить закон сопротивления поверхности турбулентному потоку Казанского-Монина к ветровому дрейфу на поверхности моря.

После перенесения на поверхностный дрейф закон имеет вид

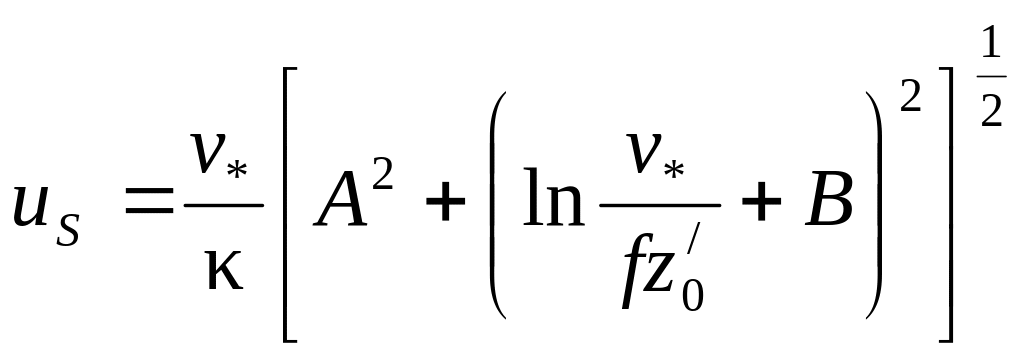; (10.9.13)

, (10.9.14)

где u_s – скорость воды на поверхности; v_* – скорость трения в воде; z^/₀ – параметр шероховатости водной поверхности по отношению к расположенному под ней течению; _S – угол между поверхностным дрейфом и наблюдаемым ветром (ветром логарифмического слоя), направление которого отождествляется с вектором трения ветра .

Если же поверхность расположена снизу потока, u_S переходит в геострофическую скорость, а - в угол между геострофической скоростью и скоростью в примыкающем к поверхности логарифмическом слое.

Значения констант остается неизменным A = 4,3; B = 1,1;  = 0,4. Величина z^/₀ определяется формулой

, (10.9.15)

где m₀ – эмпирическая константа (≈ 10^–1), _w – коэффициент кинематической вязкости (ню).

При v_* = 1 см∙с^–1; f = 10^–4 с^–1; _w = 0,012 см² с^–1 скорость дрейфа на поверхности по модели Зилитинкевича равна u_s = 40 см∙с^–1, угол отклонения от ветра _S = 16^о.

Полный перенос дрейфа направлен, как и у Экмана, под прямым углом к трению ветра. Его величина определяется средней скоростью и глубиной слоя трения

. (10.9.17)

В этой модели закон линейного возрастания коэффициента вязкости с удалением от границы распространяется на весь экмановский турбулентный пограничный слой, так что этот коэффициент достигает максимального значения там, где пограничное турбулентное течение прекращается.