Движение вдоль динамических горизонталей
Обозначим составляющие скорости через функцию тока
; (10.4.1)
; (10.4.2)
. (10.4.3)
На линии тока функция тока постоянна, следовательно, из (10.4.3)
при = const..
Движение в геострофическом течении происходит по горизонталям водного рельефа с поправкой на широту места. В баротропном море горизонтали совпадают с изобарами на горизонтальных поверхностях, поэтому линии тока на разных горизонтах будут одинаковы.
Движение вдоль изобат
Введем в уравнение геострофического течения полные потоки баротропного моря U, V:
; (10.5.1)
,
(10.5.2)
где h – глубина моря.
Проведем операцию дивергенции: продифференцируем первое уравнение по y, второе – по x и вычтем второе из первого:
; (10.5.3)
;
(10.5.4)
. (10.5.5)
Отсюда следует, что f/h = const и h/f = const, т. е. течение идет по изобатам с поправкой на широту места.
По словам Пьера Веландера, наиболее очевидный эффект топографии дна состоит в том, что она направляет глубинное течение вдоль контуров h/f. Геологи отмечали на фотографиях дна, что донные организмы под влиянием течений наклоняются и вытягиваются вдоль изобат. Этим течениям дали название контурные течения.
На рис. 10.5.1 показана карта изолиний h/f для Северной Атлантики по Веландеру.
Рис. 10.5.1. Карта изолиний h/f по Веландеру (1968)
Представим последствия того, что течение, следуя по изобатам, перетекает с участка пологого рельефа дна на участок с крутым рельефом. Очевидно, что на крутом участке изобаты сближаются, допустим, в n раз. Во столько же раз сблизятся динамические горизонтали на поверхности, за счет этого увеличится наклон уровня и скорость течения. Для сохранения постоянства расхода и неразрывности нужно, чтобы сохранилась средняя глубина. Эти условия должны строго выполнятся в баротропной среде и приблизительно – в бароклинной. С ними связано одно из распространенных географических явлений – тяготение струйных течений к материковому склону.
Расход вихренесущего геострофического течения
Среднюю между двумя станциями скорость баротропного геострофического течения можно записать
, (10.6.1)
а расход
. (10.6.2)
Подставляя первую формулу во вторую, получим весьма важное правило: расход геострофического течения не зависит от расстояния между станциями. Действительно,
. (10.6.3)
Следовательно, при неизменной глубине поперек течения (или горизонтальной отсчетной поверхности в динамическом методе) расход пропорционален разности высот изобарической поверхности (Δζ). Для бароклинной жидкости это правило соответствует формуле Якхеллна (Мамаев, 1986)
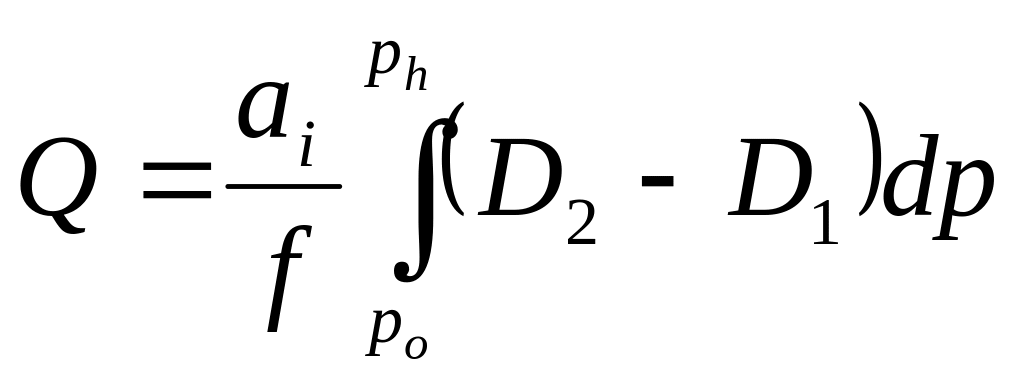. (10.6.4)
Реальное морское течение бывает заполнено вихревыми структурами. При этом уровень его поперечного сечения может быть аппроксимирован ломаной кривой. Покажем, что суммарный расход течения может быть оценен по разности высот первой и последней станции разреза, ограниченного снизу горизонтальной поверхностью (рис. 10.6.1).
Рис. 10.6.1. Схема разреза через вихренесущее течение. Результирующий расход через затемненные фигуры равен нулю. Поэтому расход через все течение определяется разностью высот крайних станций. Это верно и для разреза 1–3 справа на рисунке.
Суммарный расход внутри М-образных затемненных фигур равен нулю. Расход под огибающей точечной линией равен расходу через разрез. Прямое соединение крайних точек разреза дает ту же величину расхода. Покажем это (см. правую часть рисунка (10.6.1)).
На разрезе из трех станций (1, 2, 3) расход через сечение 1, 2, 5, 7 равен расходу через сечение 2, 5, 6, 8. Следовательно, расход через полное сечение 1, 2, 3, 4, 7 практически равен расходу через полное сечение 1, 3, 4, 7, где опускается влияние на площадь сечения отклонения в высоте станции 2. Величина этого отклонения, как правило, выражается в см или мм.