2. Моделювання вхідних впливів та збурень на еом. Математична модель у просторі

стану поліноміального впливу.

Поліноміальна функція записується у вигляді

r(t)=r0+r1t+r2t2+...+rn-1tn-1, t0.

(7.1)

Складемо систему диференційних рівнянь першого порядку, для чого вводимо позначення r=x₁ та знаходимо похідну від полінома (7.1):

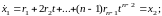
далі за аналогією матимемо:

(7.2)

Величини x_i i1,n звуться змінними (координатами) стану входа. Ці диференційні рівняння показують, що поліноміальній вхідний вплив можна отримати за допомогою інтегрування системи (7.2), або за допомогою ланцюга послідовно з`єднаних інтеграторів, як показано на рис.7.1

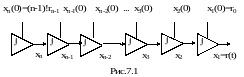
Початкові умови на інтеграторах дорівнюють:

x₁(0)=r₀;

x₂(0)=r₁;

....................

x_n(0)=r_n-1(n-1)!.

Введення матриці

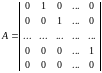
дозволяє записати векторно-матричне диференційне рівняння при

X(0)=diagxk(0).

(7.3)

Далі, згідно з розділом ІІ, необхідно обрати метод інтегрування рівняння (7.3) та записати відповідний алгоритм, який після кодування на певній мові програмування з`єднується з програмою моделі досліджуємої системи та вводиться в ЕОМ. При користуванні певним пакетом прикладних програм перед введенням в ЕОМ отримані дані по моделі вхідного впливу за допомогою вхідної мови пакета налагоджується відповідно до вимог даного пакета.

Заліковий білет № 4

1. Поняття простору стану Лінеаризація рівнянь у просторі стану та узагальнена структурна схема ок.

Припустимо, що в лінійному просторі Х_л визначено базис та установлена розміність простору n. Простір вхідних сигналів  має розмірність m n. Стан системи в даний момент часу t буде визначатися вектором Х у просторі стану. При цьому похідна від цього вектора теж є вектором і може бути розкладеним за координатами базису на n складових

В лінійному наближенні права частина диференційного рівняння на множині буде лінійною комбінацією векторів Х та U. Тоді можна записати :

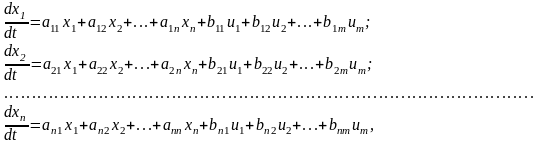
де функції a_ij та b_ik є координатами векторів Х та U.

Введемо вектори та матриці :

X(t)=[x₁(t),x₂(t),…,x_n(t)]^T ;

U(t)=[u₁(t),u₂(t),…,u_m(t)]^T ;

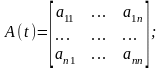
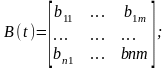
Тоді у векторно-матричній формі система диференційних рівнянь запишеться :

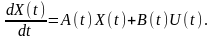(2.10)

Припустимо, що простір вихідних величин Y має розмірність r . Тоді вихід системи буде лінійною комбінацією векторів Х та U :

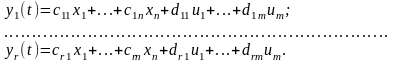
Введемо вектори та матриці

При цьому векторно-матричне рівняння має вигляд

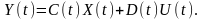(2.11)

Тоді лінійна динамічна система (кінцевовимірна та з безперервним часом) має наступну математичну модель

- рівняння стану системи; (2.12)

- рівняння виходу системи (2.13)

(рівняння вимірів).

Лінійне векторно-матричне рівняння стану динамічної системи має рішення, яке записується у наступному вигляді :

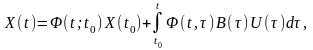(2.14)

де (t,t₀) – перехідна (фундаментальна) матриця динамічної системи;

X(t₀) – вектор початкових значень змінних стану системи.

Якщо X(t₀) =0, то у якості математичної моделі динамічної детермінованої системи можна використовувати інтеграл згортки

(2.15)

Описані трансформації виду математичних моделей динамічної детермінованої системи з безперервним часом відображені у таблиці класифікації моделей Т-2.1 у блоках : 2,3 – теоретико-множинне визначення моделі ; 4 – введення базису та координат ; 5 – модель у вигляді інтегралу згортання; та у блоці 6 – модель у вигляді векторно-матричних диференційних рівнянь. Математичні моделі, наведені у блоках 5 та 6 гарантують отримання рішень у вигляді векторів змінних стану X(t) або вимірюваного вектору Y(t).

Відповідно до формул (2.12) та (2.13) можна побудувати наступну структурну схему обєкту керування (відсутній регулятор):

Y(t)

U(t)

Z(t)