
- •Заліковий білет № 1
- •1. Характеристика електропривода як об”єкта моделювання. Математична модель у просторі “вхід-вихідних” характеристик.
- •2. Метод Зейделя.
- •Заліковий білет № 2
- •1. Декомпозиція структурної схеми привода до рівня інтегратора та складання диференційного рівняння у векторно-матричній формі.
- •2. Метод Ньютона.
- •Заліковий білет № 3
- •1. Багатомірні системи, моделюємі в просторі “вхід-вихідних” характеристик.
- •2. Моделювання вхідних впливів та збурень на еом. Математична модель у просторі
- •Заліковий білет № 4
- •1. Поняття простору стану Лінеаризація рівнянь у просторі стану та узагальнена структурна схема ок.
- •2. Математична модель у просторі стану для ступеневого (функція включення) та лінійного впливів.
- •Заліковий білет № 5
- •1. Спостережуваність та керуємість об”єктів та систем на основі математичної моделі у просторі стану.
- •2. Математична модель у просторі стану експоненціальної функції
- •Математична модель у вигляді структурної схеми багатомірної лінійної системи оптимального регулювання при детермінованому об”єкті керування.
- •2. Математичні моделі вхідних впливів у просторі стану Експоненційна функція
- •Математична модель у вигляді структурної схеми багатомірної лінійної системи оптимального регулювання при неповноій інформації про вектор стану ок.
- •2. Математична модель у просторі стану синусоїдального впливу.
- •1. Перехідна та системна матриця (приклад коливального ланцюга).
- •Моделювання випадкових та квазівипадкових послідовностей: квазівипадкові бінарні послідовності.
- •2. Моделювання двигуна постійного струму з залежним збудженням.
- •Похибки моделювання та їх облік.
- •2. Розрахунок ачх на еом: визначення матричної передавальної функції об’єкта регулювання по рівнянням стану.
- •11.1 Числове обрахування звичних диференційних рівнянь. Однокрокові методи.
- •11.2 Матриця дискретних передавальних функцій
- •12.2 Обрахування частотних характеристик сак на еом.
- •13.1 Моделювання об”єктів керування та систем на основі потенційних функцій. Рівняння Лагранжа.
- •4.1. Рівняння Лагранжа
- •13.2 Визначення ачх електроприводів (сак) на цифровій моделі: використання
- •14.1 Рівняння стану Гамільтона. Фізичний еквівалент гамільтоніану
- •14.2 Швидке перетворення Фурьє.
- •15.1 Система Гамільтона з одним ступенем свободи.
- •15.2 Алгоритм шпф для функції часу із 8 відліків.
Заліковий білет № 1
1. Характеристика електропривода як об”єкта моделювання. Математична модель у просторі “вхід-вихідних” характеристик.
Н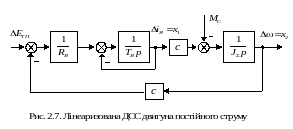 а
рисунку позначено:
а
рисунку позначено:
 -
опір якірного кола двигуна;
-
опір якірного кола двигуна;
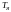 - стала часу якірного кола;
- стала часу якірного кола;
 -
коефіцієнт противо-ЕРС двигуна;
-
коефіцієнт противо-ЕРС двигуна;
 -
сумарний момент інерції рухомих частин
ЕМС (ЕП), зведений до вала двигуна.
-
сумарний момент інерції рухомих частин
ЕМС (ЕП), зведений до вала двигуна.
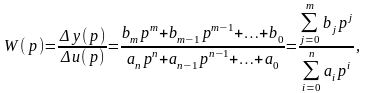 (2.26)
(2.26)
де
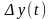 -
вихідна координата системи, яка
досліджується;
-
вихідна координата системи, яка
досліджується;
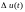 -
вхідний вплив;
-
вхідний вплив;
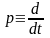 -
оператор диференціювання;
-
оператор диференціювання;
 -
відповідно, порядок знаменника та
чисельника передаточної функції, причому
-
відповідно, порядок знаменника та
чисельника передаточної функції, причому
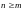 .
.
Якщо звести (2.26) до загального знаменника, а також перейти до функції часу, то стає можливим записати диференціальне рівняння n-го порядку:
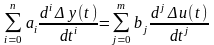 , (2.27)
, (2.27)
з
якого, шляхом введення змінних стану
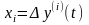 ,
здійснюється перехід до системи
диференційних рівнянь першого порядку
(у формі Коші).
,
здійснюється перехід до системи
диференційних рівнянь першого порядку
(у формі Коші).
2. Метод Зейделя.
Метод
Зейделя полягає в поелементному
знаходженні
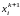 ,
але з урахуванням вже знайдених
(обчислених) величин
,
але з урахуванням вже знайдених
(обчислених) величин
 при p<i.
при p<i.
Припустимо, що всі діагональні елементи матриці A не нульові та відомий вектор Xk після k-ої ітерації. Запишемо перше рівняння системи (6.15) у вигляді
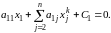
Знайдемо
x1.
Позначимо
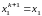 і підставимо
цю
знайдену величину в друге рівняння
системи (6.15):
і підставимо
цю
знайдену величину в друге рівняння
системи (6.15):

котре
вирішуємо відносно x2.
Позначимо
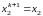 в результаті для кожної
i-ої
змінної будемо мати лінійне рівняння
з одною невідомою у вигляді:
в результаті для кожної
i-ої
змінної будемо мати лінійне рівняння
з одною невідомою у вигляді:
|
(6.16) |
Це
рівняння вирішується відносно xi,
а черговий елемент визначається як
 .
.
Щоб записати ітераційну формулу Зейделя, представимо матрицю A у вигляді:
A=D+L+V,
де D - діагональна матриця;
L - строго нижньотрикутна матриця;
V - строго верхньотрикутна матриця (для L та V усі діагональні елементи дорівнюють нулю).
При цьому на основі рівняння (6.16) система ЛАР (6.15) приймає вигляд:
(D+L)Xk+1+VXk+C=0.
Iз цієї системи знаходимо:
Xk+1=-(D+L)-1(VXk+C)=-(D+L)-1[(A-(D+L))Xk+C]=
=Xk-(D+L)-1(AXk+C)=Xk - (D+L)-1F(Xk).
Таким чином, ітераційна формула метода Зейделя записується у наступному вигляді:
Xk+1=Xk - (D+L)-1F(Xk). |
(6.17) |
Зображення цього ітераційного процесу
G(X)=X - (D+L)-1F(X).
Умови
глобального сходження метода Зейделя
визначаються нерівністю
 .
Нерівність виконується, якщо
.
Нерівність виконується, якщо
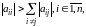 тобто
матриця A
має
домінуючу діагональ.
тобто
матриця A
має
домінуючу діагональ.
Метод Зейделя, як і метод простої ітерації, має лінійну швидкість сходження.
Заліковий білет № 2
1. Декомпозиція структурної схеми привода до рівня інтегратора та складання диференційного рівняння у векторно-матричній формі.
П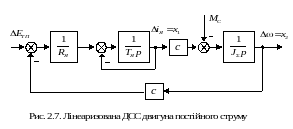 роілюструємо
такий підхід на прикладі лінеаризованої
ДСС двигуна постійного струму незалежного
збудження, наведеної на рис.2.7.
На рисунку позначено:
-
опір якірного кола двигуна;
- стала часу якірного кола;
-
коефіцієнт противо-ЕРС двигуна;
-
сумарний момент інерції рухомих частин
ЕМС (ЕП), зведений до вала двигуна.
роілюструємо
такий підхід на прикладі лінеаризованої
ДСС двигуна постійного струму незалежного
збудження, наведеної на рис.2.7.
На рисунку позначено:
-
опір якірного кола двигуна;
- стала часу якірного кола;
-
коефіцієнт противо-ЕРС двигуна;
-
сумарний момент інерції рухомих частин
ЕМС (ЕП), зведений до вала двигуна.
Якщо
вихідні сигнали інтегруючих ланок
позначити як змінні стану (струм якірного
кола
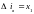 ,
а швидкість обертання вала двигуна
,
а швидкість обертання вала двигуна
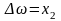 ),
то безпосередньо з ДСС можна скласти
систему нормальних диференціальних
рівнянь:
),
то безпосередньо з ДСС можна скласти
систему нормальних диференціальних
рівнянь:
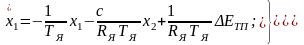 (2.23)
(2.23)
Згідно з (2.17) визначаємо матриці системи, які відповідно до (2.23) дорівнюють:
 ;
;
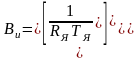 ;
;
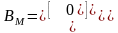 . (2.24)
. (2.24)
Таким чином, отримуємо математичний опис двигуна у векторно-матричній формі:
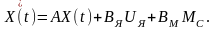 (2.25)
(2.25)

