30.Работа и кинетическая энергия.

Если на тело массы m действует постоянная сила , работа ее на перемещении 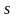т.е. равна разности кинетических энергий тела в конце и в начале перемещения.

Для этого разобьем все перемещение на малые участки, в пределах которых силу можно считать постоянной и ее работу вычислить по

,

На всем перемещении работа силы равна:

Если же на тело действуют дополнительно силы трения, получаем:

где: и - скорость тела в конце и в начале перемещения, А - работа сил трения.

Следовательно, работа силы равна:

Работа центральных сил.

Если на тело действует центральная сила , ее работа на элементарном перемещении вдоль линии действия силы равна (вдоль траектории1):

а работа на конечном перемещении:

При движении по произвольной траектории на элементарном перемещении работа силы выражается соотношением: Т.е. работа центральных сил не зависит от формы траектории, а определяется лишь начальным и конечным положениями перемещаемого тела.

Силы, работа которых не зависит от формы траектории, называют консервативными. К ним, например, относятся силы упругости, силы электростатического взаимодействия между точечными зарядами, гравитационные силы, а силы трения – не являются консервативными.

Потенциальная энергия.

Потенциальной энергией называют энергию, определяемую конфигурацией системы, относительным расположением отдельных взаимодействующих тел. выражение для потенциальной энергии для про­извольного взаимодействия записать сложно, обычно определяют ее изменение относительно уровня, условно принятого за нулевой. например, потенциальная энергия тела массы m в поле тяготения Земли, находящегося на высоте h над ее поверхностью:

а на поверхности:

Изменение потенциальной энергии тела относительно поверх­ности Земли:

При « принимает вид:

Нормировка потенциальной энергии, закон сохранения энергии.

Положим, что в замкнутой консервативной системе выделены состояния 1, 2 и 3, условно принятое за исходное, При переходе из состоя­ний 1, 2 в исходное (рис. 57) работа консервативных сил равна:

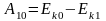
Т.е. для любых состояний системы кинетическая энергия в этом состоянии и работа внутренних сил по переходу из выбранного состояния в исходное - величина постоянная для всех состояний системы. Для расчетов важно, чтобы работа сил на любом переходе имела одинаковый знак, поэтому в выражении к значению работы надо добавить такую положительную величину , чтобы:

Сама проделанная операция выбора называется нормировкой потенциальной энергии, а сумма - потенциальной энергией системы в данном состоянии. С учетом сказанного: для всех состояний системы. Это и есть закон сохранения механичес­кой энергии.