25. Упругие силы.

Упругостью называют свойство восстанавливать времменно утраченную форму и объём, а деформациями- само изменение формы и объёма тела. Причиной упругости является наличие одновременно присутствующих сил взаимодействия между частицами тела- притяжения ( ) и отталкивания ( ). Равнодействующая этих сил равна:

На рис.46 представлены графики силы взаимного отталкивания (1), притяжения (2) и равнодействующая этих сил (3). На расстоянии между взаимодействующими частицами равнодействующая равна нулю (положение равновесия). При < преобладают силы отталкивания, а при > силы притяжения.

Потенциальная энергия взаимодействия на расстоянии между частицами:

где: .

,

Графики потенциальной энергии сил отталкивания (1), притяжения (2) и равнодействующей (3) представлены на рис.47:

Продольное сжатие и растяжение. Закон Гука.

При продольном сжатии или растяжении одного упругого образца длинны 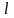и площади сечения удлинение образца определяется из опыта выражением:

где - коэффициент упругости, определяемый свойствами материала образца.

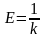Величина называется относительной деформацией. Величина , обратная коэффициенту упругости, называется модулем упругости Юнга.

С учётом этих обозначений закон Гука для деформации продольного сжатия или растяжения имеет вид:

где - называется напряжением (отношение упругих сил в деформированном образце к площади его поперечного сечения).

При изменении продольных размеров одновременно и поперечные. Изменение диаметра образца (однородного цилиндра) также подчиняется закону Гука: где: -коэффициент поперечного сжатия при продольном растяжении.

Величина называется коэффициентом Пуассона.

Если деформирующая сила изменяется от нуля до , абсолютная деформация изменяется, соответственно, от нуля до то образец приобретает потенциальную энергию упругих деформаций, численно равную работе деформирующей силы. Эта работа равна площади заштрихованной фигуры (рис.48), т.е:

Используя закон Гука, получим:

А плотность энергии, соответственно:

26. Деформация сдвига.

Деформация сдвига возникает при действии на тело касательных усилий (рис. 49). Если к верхней грани образца, имеющего форму параллелепипеда, приложена касательная сила , распределённая по грани площади , грань сдвигается на расстояние , которое называется абсолютной деформацией при сдвиге.

Относительной деформацией называют отношение абсолютной деформации к поперечным размерам . Для сдвига закон Гука принимает форму:

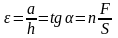
где -коэффициент сдвига, определяемый свойствами материала образца, величина, обратная , называется модулем сдвига:

Поскольку упругие деформации, для которых формулируется закон Гука, имеют место только при маленьких значениях деформации, закон Гука для сдвига принимает вид:

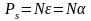
Деформация кручения.

Деформации кручения возникают при закручивании одного основания образца относительно другого .

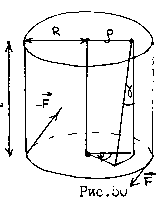
По закону Гука для этого типа деформации:ы

где - угол закручивания, - длинна образца, - момент закручивающих сил, - коэффициент кручения.

Величина называется модулем кручения т. е.

Одновременно с закручиванием образца происходит сдвиг его слоёв. Угол сдвига определяется из закона Гука.

Угол сдвига можно получить и из чисто геометрических соображений:

Сравнивая (212) и (213), получим

Момент распределённых сил, приложенных к нижнему основанию образца, получим, используя (214).

Из рис.51 видно, что элементарный момент закручивающих сил, приложенных к элементу основания, равен:

Полный момент:

Сравнивая (210) и (216), получаем связь между модулями сдвига и кручения: