Силовой анализ механизмов

2. Силы инерции звеньев плоских механизмов

Силы инерции звеньев рассматриваются как реакции звена на изменение его скорости по величине и направлению. Существование сил инерции обусловлено двумя обстоятельствами: фактом наличия у звеньев массы и фактом движения звеньев, сопровождающегося в общем случае ускорениями отдельных точек и всего звена в целом, так как известно из теоретической механики, что мерой сил инерции является произведение массы на ускорение.  Из курса теоретической механики известно, что систему сил инерции в общем случае можно привести к силе – главному вектору сил инерции   приложенного в центре масс s звена (рис. 11.6) и к паре сил, момент которой называется главным моментом сил инерции  .    Рис. 11.6  Главный вектор сил инерции определяют по формуле:  .  Главный момент сил инерции определяют по формуле:  ,  где m – масса звена, кг; а_s – ускорение цента масс, м/с²; J_s – момент инерции звена относительно оси проходящей через центр масс перпендикулярной плоскости движения, кг/м²; e - угловое ускорение звена, с^-2.  Знак «-» указывает на то, что векторы  и   соответственно направлены противоположно а_s и e.  Силы инерции звеньев совершающих вращательное движение  При равномерном вращательном движении звеньев имеющих цилиндрическую форму (рис. 11.7, а) имеем:   и  , так как соответственно а_s = 0 и e = 0.  При неравномерном вращении звеньев имеющих цилиндрическую форму имеем:   так как а_s = 0 и  , т.к. e ¹ 0.    Рис. 11.7  При равномерном вращении кривошипа (рис. 11.7, б) имеем:   так как а_s ¹ 0 и  , т.к. e = 0.  При неравномерном вращении кривошипа (рис. 11.7, в) имеем:   так как а_s ¹ 0 и  , т.к. e ¹ 0. Для удобства расчетов данную систему принято заменять одной результирующей силой инерции   приложенной в центре качания К, расположение которой определяют из выражения: .  Силы инерции звеньев совершающих поступательное движение  Если звено совершает только поступательное движение (рис. 11.8) то:   и  , так как e = 0.    Рис. 11.8  Силы инерции звеньев совершающих плоско-параллельное движение  При сложном плоско-параллельном движении звена, например шатуна в кривошипно-ползунном механизме (рис. 11.9), возникают главный вектор сил инерции   и главный момент сил инерции  .  Для удобства расчетов данную систему принято заменять одной результирующей силой инерции   приложенной в центре качания К, имеющей плечо относительно центра масс равное   и создающей момент в направлении обратном угловому ускорению шатуна e₂.    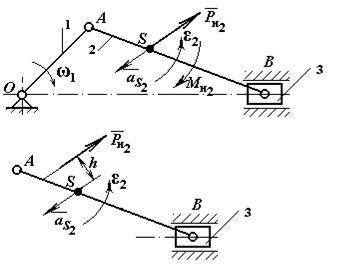Рис. 11.9 

3. Условие кинетостатической определимости плоских кинематических цепей.

 Сила, как векторная величина характеризуется относительно звеньев механизма тремя параметрами: координатами точки приложения, величиной и направлением. Рассмотрим с этих позиций реакции в кинематических парах плоских механизмов.  Число неизвестных, определенных из какой-либо сис-

темы уравнений, должно совпадать с числом уравнений.

Поэтому прежде, чем определять реакции в кинематических

парах, необходимо проверить условие кинетостатической

определимости цепи.

Для каждого звена кинематической цепи, имеющего

плоскопараллельное движение, можно записать три уравне-

ния равновесия. Для n звеньев цепи число уравнений будет

3n. Число неизвестных для каждой пары V класса равно

двум: модуль реакции и угол a (рис.2.3,а). Для высшей пары

– одному: модуль реакции (рис.2.3,б).

И условие кинетостатической определимости для пло-

ской кинематической цепи:

5 4

3n = 2 p - p . (2.3)

А для группы Ассура, где одни низшие пары: 3n = 2 p5

2.3а 2.3б

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл.).

 

Кинематические пары	Равновесие каждого звена	Известные параметры	Неизвестные параметры
5-й класс Вращательная		Точка приложения	Величина, направление
Поступательная		Направление	Величина, точка приложения
4-й класс		Точка приложения, направление	Величина

Примечание. 2, 3, 5 – номера звеньев.

 

В кинематических парах 5-го класса известно по одному параметру сил реакций, неизвестны два, в кинематических парах 4-го класса известны два параметра, а неизвестен один.

Таким образом, плоская кинематическая цепь, состоящая из кинематических пар 5-го и 4-го классов, имеет 2Р₅ + Р₄ неизвестных величин сил реакций.

В то же время для одного звена можно составить 3 уравнения статики, а для n звеньев – 3n уравнений статики.

Кинематическая цепь будет статически определима, если число неизвестных величин сил реакций не превышает числа возможных уравнений статики, т.е.

3n = 2P₅ + Р₄.

Это и есть условие статической определимости кинематической цепи.

Полученное равенство можно записать в виде

3n – 2Р₅ – Р₄ = 0.

Но запись слева от знака равенства является числом степеней свободы кинематической цепи W, т.е.

W = 3n – 2Р₅ – P₄ = 0.

Как известно таким свойством (W=0) обладают структурные группы, или группы Ассура – статически определимые кинематические цепи.

 

Пример 1.

Задан шестизвенный рычажный механизм (рис. 4.4), состоящий из начального механизма (звенья 0 и 1) и структурных групп, образованных звеньями 2 и 3 (двухповодковая структурная группа 2-го класса, 1-го вида) и 4, 5 (структурная группа 2-го класса, 2-го вида).

                          Рис. 4.4. Шестизвенный рычажный механизм

 

Решение.

Проводим силовой расчёт структурной группы 4-5 (определяем неизвестные реакции, если известны внешние силы, действующие на звенья 4 и 5):

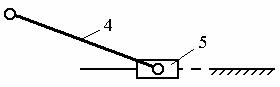
Проводим силовой расчёт структурной группы 2-3:

Проводим силовой расчёт ведущего звена: