1.Матрицы.Операции с матрицами.

Прямоугольной матрицей называется таблицей чисел в m(строк) n(столбцов).

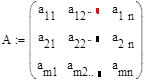
Матрица у которой число строк равно числу столбцов называется квадратной

Квадратная матрица у которой все элементы равны нулю кроме главной диаконали называется диагональной

Нулевая матрица –это матрица где все нули.

Единичная матрица- на главное диагонали стоят единицы.

Матрица приведенная к верхнему треугольному виду- это матрица у которой ниже главной диагонали нули.

Матрица приведенная к нижнему треугольному виду- это матрица у которой выше глав. диагонали нули.

Операции с матрицами.

1. Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц А и B называется матрица С у которой элементы cij=aij+bij .

Am*n=(aij) i= 1,2…m

J=1,2…n

Bm*n=(bij) i= 1,2…m

J=1,2…n

Cm*n=(cij) i= 1,2…m

J=1,2…n

Cij=aij+bij

Свойства

1. Коммутативность

A+B=B+A

2. Ассоциативность

A+(B+C)=(A+B)+C

3. Существование нулевого элемента

Существует нулевая матрица ,такая что A+нулевая матрица=A

4.Существует матрица B такая что A+B=нулевая матрица.

2) Умножение на число

Произведение матрицы на число называется матрица В у которой элементы bij=k*aij

Свойства

1. Число(A+B)=ЧислоA+ЧислоB

2. (Число+M)*A=число А+МА

3. Транцпонирование

Суть: строки становятся столбцами

Матрица называется симметрической если ее элементы симметрично равны относительно главной диагонали.

4)Умножение матриц

Чтобы матрицы перемножились необходимо чтобы количество столбцов матрицы слева равнялось количеству строк матрицы справа.

Каждую строку слева умножим каждый столбец матрицы справа= (а11в11+а12в21+а13в31;а11в12+а12в22+а13+в33; а11в13+а12в23+а13в33)

Свойства

1. А*Вне равноВ*А кроме когда А=В

2. Существует единичная матрица такая что, А* единичную матрицу=А

3. А*(В+С)=АВ+АС

4. А*(В*С)=(А*В)*С

5. С=А*В Ст=Вт*Ат

2. Определители. И их свойства.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ— число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу.

Определитель характерен только для квадратной матрицы. Если определитель матрицы не равен нулю, то матрица называется невырожденной.

Свойства:

1. При умножение всех элементов строке определителя на число опредилитель умножается на число.

2)Определитель матрицы с нулевой строкой равен нулю.

3) При перестановке двух строк определителя местами определитель меняет знак

4) Если две строки определителя равны, то определитель равен нулю.

5) Если i-я строка матрицы представляется в виде суммы двух векторов a+b , то ее определитель есть сумма двух определителей отличающихся i-ой строкой у одного из них i-я строка это вектор а у второго вектор b.

6) Определитель не меняет знак если к какой либо-нибудь из строк определителя добавить другую строку определителя умноженное на число

7) Определитель транспорированной матрицы равен определителю матрицы.

Эти свойства характерны и для столбцов.

3.Вычисление определителей 1,2,3,4, n-ого порядков.

Вычисление определителей первого порядка.

Матрица размера это просто число. Определителем такой матрицы является само это число.

Вычисление определителей второго порядка.

Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.

Вычисление определителей третьего порядка.

Определитель третьего порядка вычисляется по правилу:

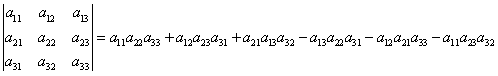
Вычислить определитель 4го порядка

Определитель находится путем приведение определителя к верхнему треугольному виду, после перемножаем элементы на главной диагонали.