5.2. Метрологические характеристики средств измерений

Метрологическая характеристика (МХ) средства измерений – характеристика одного или нескольких свойств СИ, влияющая на результат измерений или его характеристики. Метрологические характеристики средств измерений, которые установлены в нормативных документах, называются нормированными, а определенные экспериментально  действительными.

К основным метрологическим характеристикам СИ относятся:

 деление шкалы – промежуток между двумя соседними отметками шкалы СИ;

 цена деления шкалы – разность значений величины, соответству-ющих двум соседним отметкам шкалы СИ. Цена деления шкалы связана с числом делений и погрешностью ИП;

– начальное и конечное значения шкалы – наименьшее и наибольшее значение измеряемой величины, которое может быть отсчитано по шкале СИ;

– диапазон показаний СИ – область значений шкалы прибора, ограниченная начальным и конечным значениями шкалы;

 диапазон измерений СИ – область значений ФВ, в пределах которой нормированы допустимые погрешности средств измерений. Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа), называют соответственно нижним и верхним пределом измерений. Например, у шкалы на рис. 5.2 начальный участок (~20 %) сжат, поэтому производить отсчеты на нем неудобно. В этом случае предел измерения по шкале составляет 50 ед., диапазон – 1050 ед.;

Рис. 5.2. Неравномерная шкала СИ

• номинальное значение меры – значение величины, приписанное мере при ее изготовлении (часто оно указано на мере);

• действительное значение меры – значение величины, приписанное мере при ее калибровке и поверке. Государственный эталон единицы массы имеет действительное значение 1,00000087 кг;

• показание СИ – значение величины на показывающем устройстве средства измерений;

• чувствительность СИ (S) – свойство, определяемое отношением изменений входного сигнала этого средства к вызывающему его изменению измеряемой величины. Различают абсолютную S и относительную S_o чувствительность, которые определяются по формулам:

S = y / x, S_о = y / (x / х), (5.1)

где y  изменение величины на выходе средства измерений; x  изменение измеряемой величины; х – измеряемая величина;

• порог чувствительности СИ – характеристика СИ в виде наименьшего значения изменения ФВ, с которого может осуществляться ее измерение данным СИ;

• смещение нуля – показание СИ, отличное от нуля при входном сигнале, равном нулю;

• дрейф показаний СИ – изменение показаний СИ во времени, обусловленное изменением влияющих величин или других факторов;

• погрешность СИ – разность между показанием СИ и истинным (или действительным) значением измеряемой ФВ. Классификация погрешностей СИ приведена на рис. 5.3.

• 

По способу формирования

По способу выявления

По внешним воздействиям

абсолютная

случайная

основная

относительная

систематическая

дополнительная

приведенная

По характеру режима измерений

По взаимодействию с выходным сигналом

статическая

динамическая

мультипликативная

аддитивная

Рис. 5.3. Классификация погрешностей средств измерений

Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные. Под основной понимают погрешность СИ, которое применяется в нормальных условиях. Как правило, нормальными условиями эксплуатации являются температура (20 ± 5) ^оС, относительная влажность воздуха (65 ± 15) %, атмосферное давление от 97 до 104 кПа.

Дополнительная погрешность СИ – составляющая погрешности СИ, возникающая дополнительно к основной погрешности вследствие отклонений какой-либо из влияющих величин от нормального ее значения или вследствие выхода этой величины за пределы нормальной области значений.

Систематическая погрешность СИ – составляющая общей погрешности, которая остается постоянной или закономерно изменяется при многократных измерениях одной и той же величины.

Случайной погрешностью СИ называют составляющую общей погрешности, изменяющуюся при повторных изменениях одной и той же величины случайным образом.

Статические погрешности возникают при измерении постоянных величин после завершения переходных процессов в элементах СИ. Погрешность СИ, возникающая при измерении изменяющейся ФВ, называется динамической. Под абсолютной понимают погрешность СИ, выраженную в единицах измеряемой ФВ и определяемую по уравнению

Δ = Х_п – Х_д, (5.2)

где Х_п – показание прибора; Х_д – действительное значение ФВ.

В качестве Х_д принимают либо номинальное значение (значение меры), либо значение величины, измеренной более точным СИ. Абсолютная погрешность выражается в единицах измеренной ФВ и может быть задана:

• либо одним числом: Δ = ±а (линия 1 на рис. 5.4);

• либо в виде линейной зависимости Δ = ±bх (линия 2), Δ = ±(а + bх) (линии 3);

• либо в виде функции Δ = f(x).

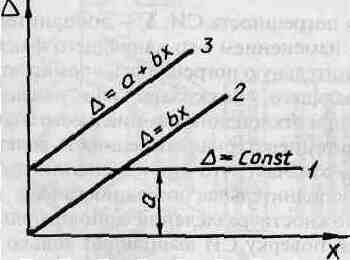
Рис. 5.4. Формирование аддитивной и мультипликативной составляющих погрешности

Если значение погрешности не изменяется во всем диапазоне измерений (линия 1), такая погрешность называется аддитивной (или погреш-ностью нуля). Если погрешность изменяется пропорционально измеряемой величине, ее называют мультипликативной (линия 2). В большинстве случаев аддитивная и мультипликативная составляющие присутствуют одновременно (линия 3).

Абсолютная погрешность не всегда позволяет сравнить СИ по точности измерений. Для этой цели используют относительную погрешность δ как отношение абсолютной погрешности СИ к результату измерений или действительному значению измеренной ФВ:

. (5.3)

Из формулы (5.3) следует, что для одного и того же СИ относительная погрешность δ уменьшается с ростом Х_п., то есть, при измерении на начальном участке шкалы с начальной нулевой отметкой погрешность измерения может быть сколь угодно велика, чем объясняется запрет измерений на таких участках шкалы СИ.

Выбор вида нормирования погрешности зависит от характера ее изменения по диапазону измерения. Если СИ имеет только аддитивную составляющую (или мультипликативной можно пренебречь), то предел допускаемой абсолютной погрешности Δ = const, a δ будет изменяться по гиперболе. В этом случае удобнее нормировать абсолютную погрешность Δ = ±а. В СИ с преобладающей мультипликативной погрешностью удобнее нормировать предел допустимой относительной погрешности

δ = ±с = const.

Нормирование только абсолютной погрешности не позволяет сравнивать по точности СИ, различающиеся пределом измерений, нормирование относительной погрешности также ограничено из-за непостоянства величины δ. Поэтому в большинстве случаев нормируют приведенную погрешность СИ – относительную погрешность, которая выражается отношением абсолютной погрешности СИ к условно принятому значению величины, постоянному во всем диапазоне измерений или в его части. Приведенную погрешность (в %) определяют по формуле

, (5.4)

где Х_N – нормирующее значение, которое выбирают в зависимости от вида и характера шкалы прибора.

Если нулевое значение входного сигнала находится на краю или вне диапазона измерений, то нормирующее значение х_N для СИ с равномерной или степенной шкалой определяется по большему из пределов измерений. Если нулевое значение находится внутри диапазона измерений, то X_N принимается равным большему из модулей в пределе измерений. Для средств измерений физической величины, для которой принята шкала с условным нулем, нормирующее значение принимают равным модулю разности пределов измерений. Например, для милливольтметра термоэлектрического термометра с пределами измерений 200…600 ^оС нормирующее значение Х_N = 400 ^оC. Для средств измерений с установленным номинальным значением нормирующее значение принимают равным этому номинальному значению. Например, для частотомеров с диапазоном измерений 4555 Гц и номинальным значением 50 Гц нормирующее значение Х_N = 50 Гц.

Точность СИ – характеристика качества СИ, отражающая близость его погрешности к нулю. К точностным характеристикам СИ относят погрешность СИ, нестабильность, порог чувствительности, дрейф нуля. Обобщенной характеристикой точности для данного типа СИ является класс точности, который может выражаться допустимой основной и дополнительной погрешностями, а также другими характеристиками, влия-ющими на точность. Класс точности дает возможность судить о том, в каких пределах находится погрешность СИ одного типа, но при этом не является непосредственно показателем точности измерений, выполняемых этими средствами, что необходимо учитывать при выборе СИ.

в зависимости от характера измерения границ абсолютных погреш-ностей СИ конкретного вида, а также от свойств и назначения этих средств измерений пределы допускаемых погрешностей выражаются в виде:

• приведенных погрешностей, если указанные границы можно полагать практически неизменными;

• относительных погрешностей, если указанные границы нельзя полагать постоянными;

• абсолютных погрешностей, если погрешности результатов в данной области измерений принято выражать в единицах измеряемой величины или делениях шкалы.

Предел допускаемой абсолютной погрешности находят по формуле

 = а = Р (5.5)

или

 =  (а + вх), (5.6)

где х – значение измеряемой величины на входе средств измерений; а и в – положительные числа, не зависящие от х.

Пределы допускаемой приведенной основной погрешности определяют по формуле

 = 100 =  р, (5.7)

где  – пределы допускаемой абсолютной погрешности, устанавливаемые по формуле (5.6); Х_N – нормирующее значение, выраженное в единицах измеряемой величины; р – отвлеченное положительное число, выбираемое из следующего ряда: 1  10ⁿ; 1,5  10ⁿ; 1,6  10ⁿ; 2  10ⁿ; 2,5  10ⁿ; 3  10ⁿ; 4  10ⁿ; 5  10ⁿ; 6  10ⁿ (где n = 1; 0; –1; –2 и т. д.).

Пределы допускаемой относительной погрешности вычисляют по формуле

 = 100 =  g, (5.8)

где g – отвлеченное положительное число, выбираемое из ряда, аналогичного ряду для р.

Если предел допускаемой абсолютной погрешности  определяли по формуле (5.5) или по формуле (5.6), то

 = = [c + d ( – 1), (5.9)

где Х_к – больший (по модулю) из пределов измерений; с и d – положительные числа, выбираемые из ряда предпочтительных чисел:

c = b + d; d = . (5.10)

Обозначения класса точности наносятся на циферблат и корпус средства измерения, приводятся в нормативной документации. Для обозначений могут быть использованы прописные буквы латинского алфавита (М, С и т. д.) или римские цифры. В этих случаях предел допускаемой основной погрешности обычно выражают через абсолютную погрешность.

Для средств измерений с равномерной шкалой, у которых нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, обозначение класса точности арабскими цифрами означает, что значение измеряемой величины не отличается от значения, которое показывает указатель отсчетного устройства, более чем на соответству-ющее число процентов от верхнего предела измерений.

Пример 3. Указатель отсчетного устройства вольтметра с равномерной шкалой класса точности 0,5 показывает значение 124 В. Чему равно измеряемое напряжение, если верхний предел измерений 200 В?

Решение. Предел допускаемой приведенной погрешности 0,5. По формуле (5.7) находим

U = (124  1) В.

Для оценки качества и эффективности СИ используют и ряд других характеристик: потребление электроэнергии, стабильность характеристик, защищенность от внешних влияний, габариты, масса, стоимость и др.