Коэффициенты Стьюдента

Число измерений n	Доверительная вероятность Рд
	0,80	0,90	0,95	0,99
2	3,080	6,310	12,710	63,700
3	1,886	2,920	4,300	9,920
4	1,638	2,350	3,188	5,840
5	1,533	2,130	2,770	4,600
6	1,476	2,020	2,570	4,030
7	1,440	1,940	2,450	3,710
8	1,415	1,860	2,360	3,500
9	1,397	1,830	2,310	3,360
10	1,383	1,800	2,260	3,250

Пусть, например, выполнено девять измерений величины и получено среднее значение = 170 мм, среднеквадратическое отклонение  = 3,1 мм. Требуемую точность измерений можно определить для разных уровней доверительной вероятности: µ = ±1,9 мм (Р = 0,9); µ = ± 2,4 мм (Р = 0,95); µ = ± 3,5 (Р = 0,99). При уменьшении доверительной вероятности на 10 % точность результата возрастает примерно на 44 %. Точность измерений зависит от числа измерений. Например, увеличение изменений в 4 раза вызывает увеличение точности в 2 раза.

Относительную погрешность результатов серии измерений при заданной доверительной вероятности находят по формуле

%. (4.11)

При обработке результатов измерений возникает необходимость исключить грубые ошибки измерений (промахи) – заведомо неправильный результат, возникающий из-за нарушения основных условий измерения или недосмотра экспериментатора.

Грубые ошибки необходимо отбрасывать. Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от остальных значений.

Грубые ошибки отбраковываются путем определения специальных критериев.

Пусть имеется число измерений (n + 1), при этом n не вызывают сомнения, одно измерение нарушает ряд измерений. Все измерения располагают в порядке возрастания, тогда сомнительный результат Х_п + 1 или Х_п  1.

Находим среднее арифметическое значение n измерений

.

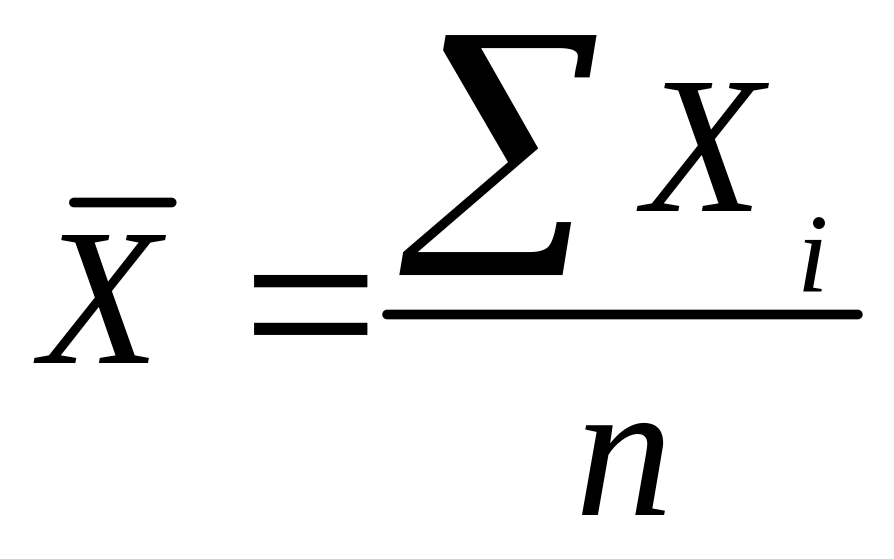Определяем среднюю квадратическую погрешность

.

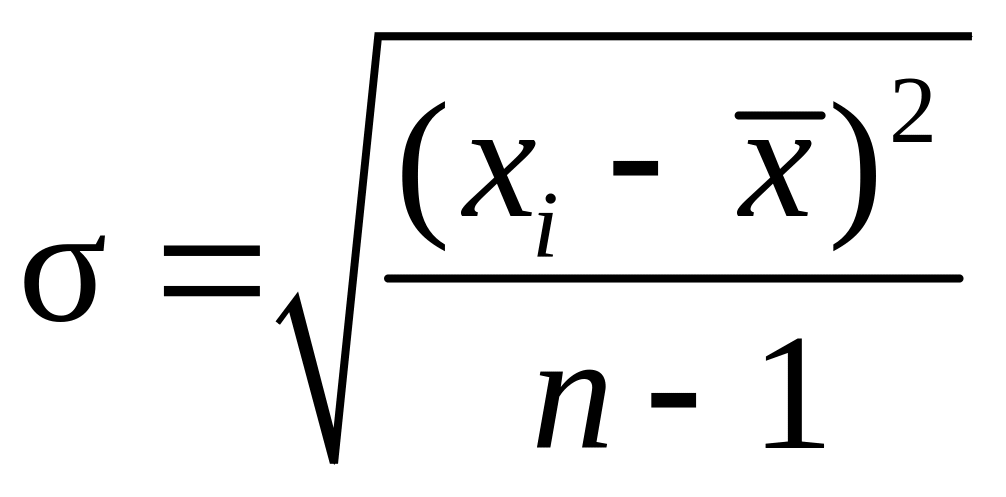Исходя из степени достоверности, которая должна быть обеспечена, зададимся вероятностью того, что значение не превышает некоторого значения ε (допустимое значение интервала), которое определяем по формуле

ε = t σ. (4.12)

Если > ε, результат Х_п + 1  промах, который следует исключить.

Пример 1. В результате измерений были получены следующие значения: 81, 80, 80, 82, 87.

Находим:

 среднее значение = 80,8;

 среднеквадратическое отклонение σ = 0,96;

 допустимое значение интервала ε = 2,26.

Так как разность 87  82 > 2,26, значение 87 – промах, который исключается при обработке результатов.

Промах можно определить с помощью критерия Диксона (K_Д). Все результаты измерений располагают в порядке возрастания. Если величина, которая вызывает сомнение Х₁, то K_Д определяют по формуле

(4.13)

Если величина, которая вызывает сомнение, Х_п + 1, то K_Д определяют по формуле

. (4.14)

Если K_Д больше табличного значения Z_p (табл. 4.3), то результат, который вызывает сомнение, является грубой ошибкой.

Таблица 4.3

Число степеней свободы (n – 1)	Zp при Р
	0,90	0,95	0,99
3	0,58	0,75	0,89
4	0,56	0,64	0,78
5	0,48	0,56	0,70
6	0,35	0,41	0,53

Пример 2. В результате измерений были получены следующие значения: 81, 80, 80, 82, 87. Располагаем их по возрастанию: 80, 80, 81, 82, 87, затем по формуле (4.14) находим K_Д = 0,71. Табличное значение Zp = 0,64. Значение коэффициента Диксона превышает табличное значение (0,71 > 0,64), значит, 87 – промах.

Если число измерений невелико (не более 10), то для оценки промаха можно использовать критерий Шовине. В этом случае промахом будет считаться результат Х_i, если разность | – X_i| превышает значения, приведенные ниже:

| – Х_i|  1,6 при n = 3;

| – Х_i|  1,7  при n = 6;

| – Х_i|  1,9 при n = 8;

| – Х_i|  2,0 при n = 1.0

Контрольные вопросы

1. Как классифицируются методы измерений?

2. В чем сущность нулевого метода измерения?

3. Как требования регламентируются МВИ?

4. Каков порядок аттестации методики выполнения измерений?

5. Как классифицируются погрешности измерений?

6. Как можно уменьшить размер случайной погрешности измерений?

7. Как определяются промахи?

8. От чего зависит величина доверительного интервала?